Free Energy Projective Simulation (FEPS): Active inference with interpretability

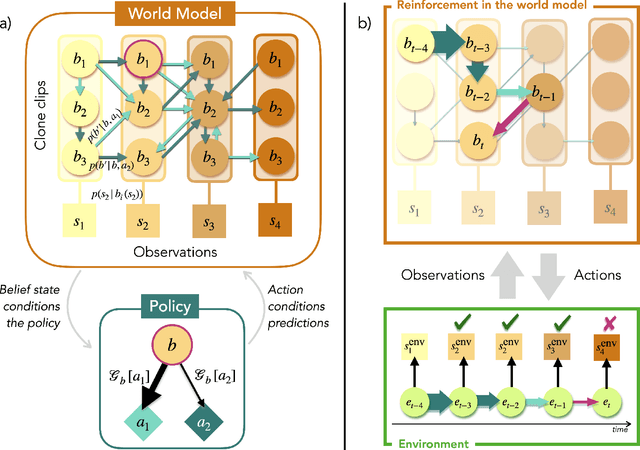
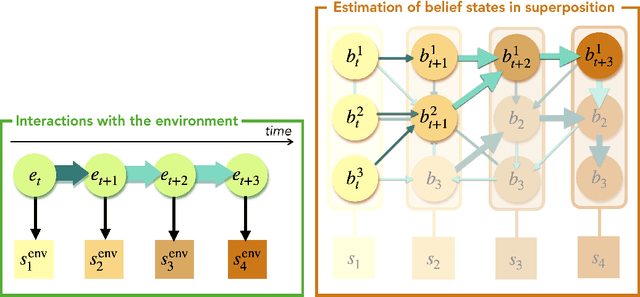
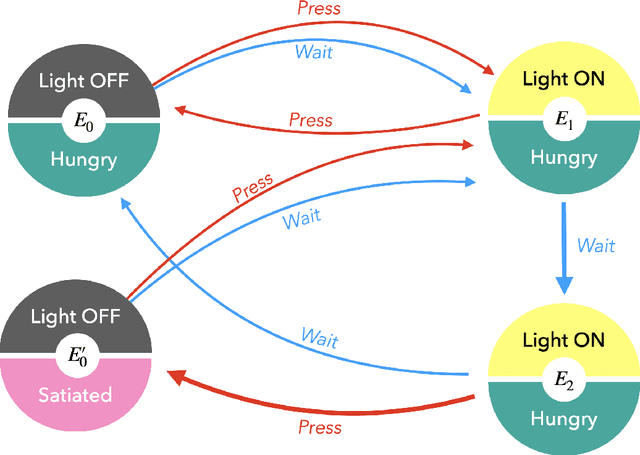
In the last decade, the free energy principle (FEP) and active inference (AIF) have achieved many successes connecting conceptual models of learning and cognition to mathematical models of perception and action. This effort is driven by a multidisciplinary interest in understanding aspects of self-organizing complex adaptive systems, including elements of agency. Various reinforcement learning (RL) models performing active inference have been proposed and trained on standard RL tasks using deep neural networks. Recent work has focused on improving such agents' performance in complex environments by incorporating the latest machine learning techniques. In this paper, we take an alternative approach. Within the constraints imposed by the FEP and AIF, we attempt to model agents in an interpretable way without deep neural networks by introducing Free Energy Projective Simulation (FEPS). Using internal rewards only, FEPS agents build a representation of their partially observable environments with which they interact. Following AIF, the policy to achieve a given task is derived from this world model by minimizing the expected free energy. Leveraging the interpretability of the model, techniques are introduced to deal with long-term goals and reduce prediction errors caused by erroneous hidden state estimation. We test the FEPS model on two RL environments inspired from behavioral biology: a timed response task and a navigation task in a partially observable grid. Our results show that FEPS agents fully resolve the ambiguity of both environments by appropriately contextualizing their observations based on prediction accuracy only. In addition, they infer optimal policies flexibly for any target observation in the environment.

A Universal Quantum Computer From Relativistic Motion

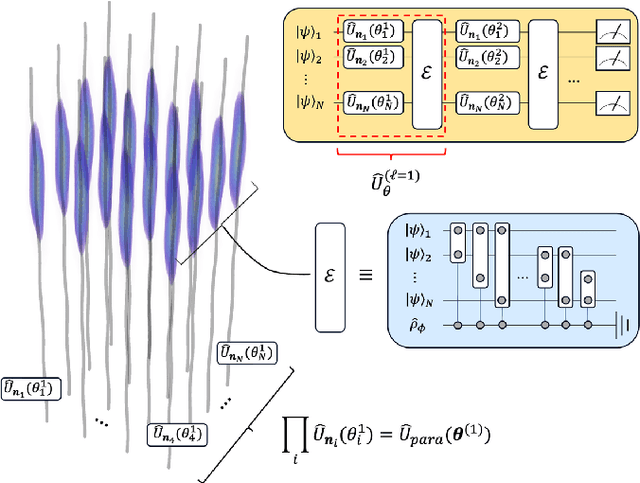
We present an explicit construction of a relativistic quantum computing architecture using a variational quantum circuit approach that is shown to allow for universal quantum computing. The variational quantum circuit consists of tunable single-qubit rotations and entangling gates that are implemented successively. The single qubit rotations are parameterized by the proper time intervals of the qubits' trajectories and can be tuned by varying their relativistic motion in spacetime. The entangling layer is mediated by a relativistic quantum field instead of through direct coupling between the qubits. Within this setting, we give a prescription for how to use quantum field-mediated entanglement and manipulation of the relativistic motion of qubits to obtain a universal gate set, for which compact non-perturbative expressions that are valid for general spacetimes are also obtained. We also derive a lower bound on the channel fidelity that shows the existence of parameter regimes in which all entangling operations are effectively unitary, despite the noise generated from the presence of a mediating quantum field. Finally, we consider an explicit implementation of the quantum Fourier transform with relativistic qubits.

Multi-Excitation Projective Simulation with a Many-Body Physics Inspired Inductive Bias

With the impressive progress of deep learning, applications relying on machine learning are increasingly being integrated into daily life. However, most deep learning models have an opaque, oracle-like nature making it difficult to interpret and understand their decisions. This problem led to the development of the field known as eXplainable Artificial Intelligence (XAI). One method in this field known as Projective Simulation (PS) models a chain-of-thought as a random walk of a particle on a graph with vertices that have concepts attached to them. While this description has various benefits, including the possibility of quantization, it cannot be naturally used to model thoughts that combine several concepts simultaneously. To overcome this limitation, we introduce Multi-Excitation Projective Simulation (mePS), a generalization that considers a chain-of-thought to be a random walk of several particles on a hypergraph. A definition for a dynamic hypergraph is put forward to describe the agent's training history along with applications to AI and hypergraph visualization. An inductive bias inspired by the remarkably successful few-body interaction models used in quantum many-body physics is formalized for our classical mePS framework and employed to tackle the exponential complexity associated with naive implementations of hypergraphs. We prove that our inductive bias reduces the complexity from exponential to polynomial, with the exponent representing the cutoff on how many particles can interact. We numerically apply our method to two toy environments and a more complex scenario modelling the diagnosis of a broken computer. These environments demonstrate the resource savings provided by an appropriate choice of inductive bias, as well as showcasing aspects of interpretability. A quantum model for mePS is also briefly outlined and some future directions for it are discussed.

Variational measurement-based quantum computation for generative modeling

Measurement-based quantum computation (MBQC) offers a fundamentally unique paradigm to design quantum algorithms. Indeed, due to the inherent randomness of quantum measurements, the natural operations in MBQC are not deterministic and unitary, but are rather augmented with probabilistic byproducts. Yet, the main algorithmic use of MBQC so far has been to completely counteract this probabilistic nature in order to simulate unitary computations expressed in the circuit model. In this work, we propose designing MBQC algorithms that embrace this inherent randomness and treat the random byproducts in MBQC as a resource for computation. As a natural application where randomness can be beneficial, we consider generative modeling, a task in machine learning centered around generating complex probability distributions. To address this task, we propose a variational MBQC algorithm equipped with control parameters that allow to directly adjust the degree of randomness to be admitted in the computation. Our numerical findings indicate that this additional randomness can lead to significant gains in learning performance in certain generative modeling tasks. These results highlight the potential advantages in exploiting the inherent randomness of MBQC and motivate further research into MBQC-based algorithms.

Reinforcement learning and decision making via single-photon quantum walks

Variational quantum algorithms represent a promising approach to quantum machine learning where classical neural networks are replaced by parametrized quantum circuits. Here, we present a variational approach to quantize projective simulation (PS), a reinforcement learning model aimed at interpretable artificial intelligence. Decision making in PS is modeled as a random walk on a graph describing the agent's memory. To implement the quantized model, we consider quantum walks of single photons in a lattice of tunable Mach-Zehnder interferometers. We propose variational algorithms tailored to reinforcement learning tasks, and we show, using an example from transfer learning, that the quantized PS learning model can outperform its classical counterpart. Finally, we discuss the role of quantum interference for training and decision making, paving the way for realizations of interpretable quantum learning agents.