Operationally meaningful representations of physical systems in neural networks
Paper and Code
Jan 02, 2020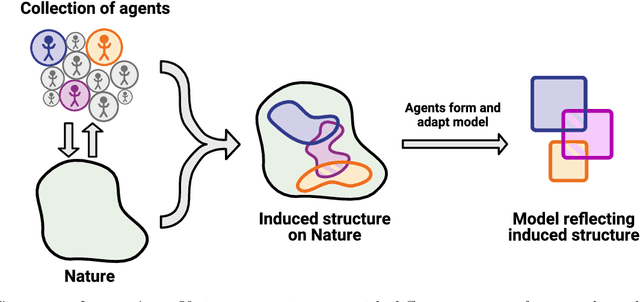
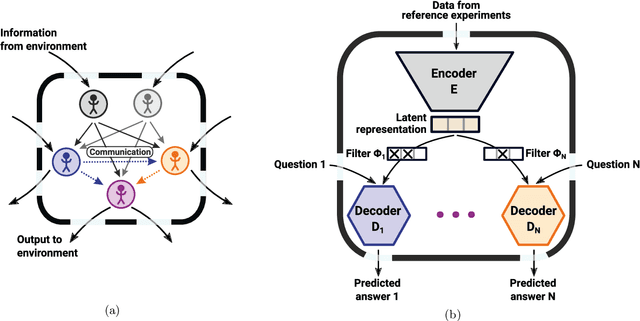
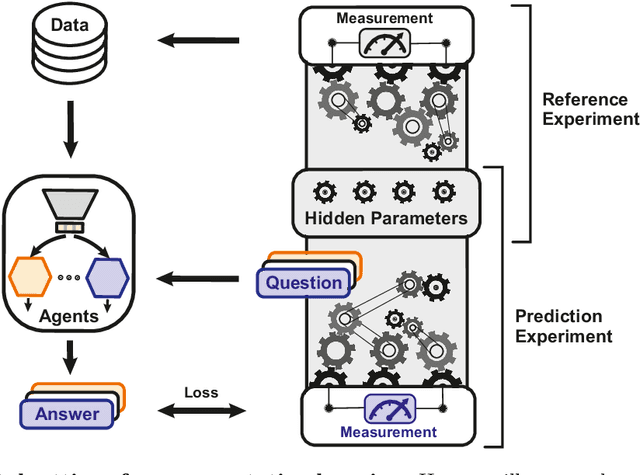
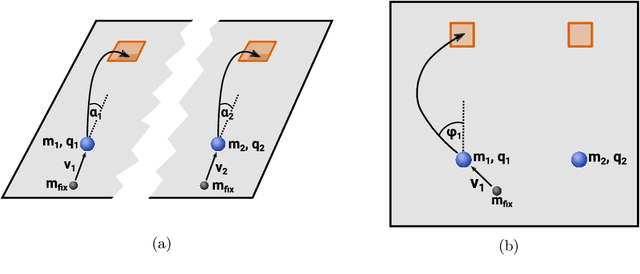
To make progress in science, we often build abstract representations of physical systems that meaningfully encode information about the systems. The representations learnt by most current machine learning techniques reflect statistical structure present in the training data; however, these methods do not allow us to specify explicit and operationally meaningful requirements on the representation. Here, we present a neural network architecture based on the notion that agents dealing with different aspects of a physical system should be able to communicate relevant information as efficiently as possible to one another. This produces representations that separate different parameters which are useful for making statements about the physical system in different experimental settings. We present examples involving both classical and quantum physics. For instance, our architecture finds a compact representation of an arbitrary two-qubit system that separates local parameters from parameters describing quantum correlations. We further show that this method can be combined with reinforcement learning to enable representation learning within interactive scenarios where agents need to explore experimental settings to identify relevant variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge