Compilation of product-formula Hamiltonian simulation via reinforcement learning

Hamiltonian simulation is believed to be one of the first tasks where quantum computers can yield a quantum advantage. One of the most popular methods of Hamiltonian simulation is Trotterization, which makes use of the approximation $e^{i\sum_jA_j}\sim \prod_je^{iA_j}$ and higher-order corrections thereto. However, this leaves open the question of the order of operations (i.e. the order of the product over $j$, which is known to affect the quality of approximation). In some cases this order is fixed by the desire to minimise the error of approximation; when it is not the case, we propose that the order can be chosen to optimize compilation to a native quantum architecture. This presents a new compilation problem -- order-agnostic quantum circuit compilation -- which we prove is NP-hard in the worst case. In lieu of an easily-computable exact solution, we turn to methods of heuristic optimization of compilation. We focus on reinforcement learning due to the sequential nature of the compilation task, comparing it to simulated annealing and Monte Carlo tree search. While two of the methods outperform a naive heuristic, reinforcement learning clearly outperforms all others, with a gain of around 12% with respect to the second-best method and of around 50% compared to the naive heuristic in terms of the gate count. We further test the ability of RL to generalize across instances of the compilation problem, and find that a single learner is able to solve entire problem families. This demonstrates the ability of machine learning techniques to provide assistance in an order-agnostic quantum compilation task.

Automated Gadget Discovery in Science

In recent years, reinforcement learning (RL) has become increasingly successful in its application to science and the process of scientific discovery in general. However, while RL algorithms learn to solve increasingly complex problems, interpreting the solutions they provide becomes ever more challenging. In this work, we gain insights into an RL agent's learned behavior through a post-hoc analysis based on sequence mining and clustering. Specifically, frequent and compact subroutines, used by the agent to solve a given task, are distilled as gadgets and then grouped by various metrics. This process of gadget discovery develops in three stages: First, we use an RL agent to generate data, then, we employ a mining algorithm to extract gadgets and finally, the obtained gadgets are grouped by a density-based clustering algorithm. We demonstrate our method by applying it to two quantum-inspired RL environments. First, we consider simulated quantum optics experiments for the design of high-dimensional multipartite entangled states where the algorithm finds gadgets that correspond to modern interferometer setups. Second, we consider a circuit-based quantum computing environment where the algorithm discovers various gadgets for quantum information processing, such as quantum teleportation. This approach for analyzing the policy of a learned agent is agent and environment agnostic and can yield interesting insights into any agent's policy.

Reinforcement learning for optimization of variational quantum circuit architectures

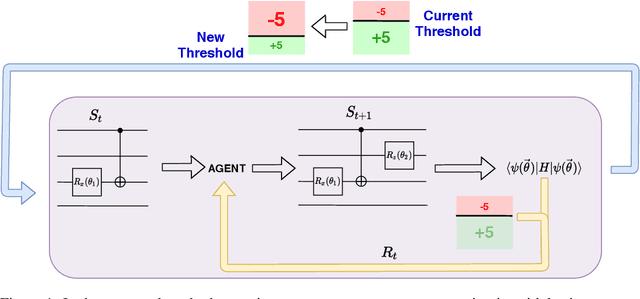
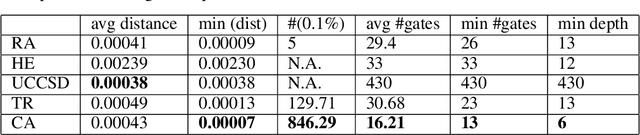
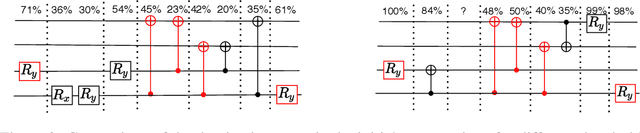
The study of Variational Quantum Eigensolvers (VQEs) has been in the spotlight in recent times as they may lead to real-world applications of near-term quantum devices. However, their performance depends on the structure of the used variational ansatz, which requires balancing the depth and expressivity of the corresponding circuit. In recent years, various methods for VQE structure optimization have been introduced but the capacities of machine learning to aid with this problem has not yet been fully investigated. In this work, we propose a reinforcement learning algorithm that autonomously explores the space of possible ans{\"a}tze, identifying economic circuits which still yield accurate ground energy estimates. The algorithm is intrinsically motivated, and it incrementally improves the accuracy of the result while minimizing the circuit depth. We showcase the performance of our algorithm on the problem of estimating the ground-state energy of lithium hydride (LiH). In this well-known benchmark problem, we achieve chemical accuracy, as well as state-of-the-art results in terms of circuit depth.

Operationally meaningful representations of physical systems in neural networks

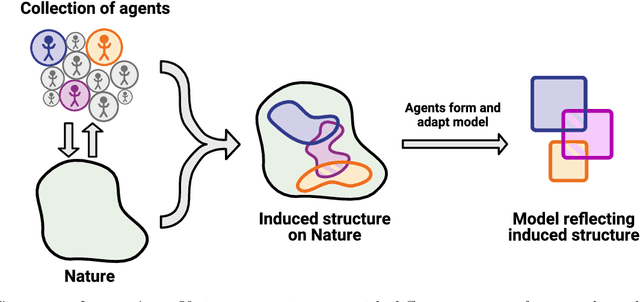
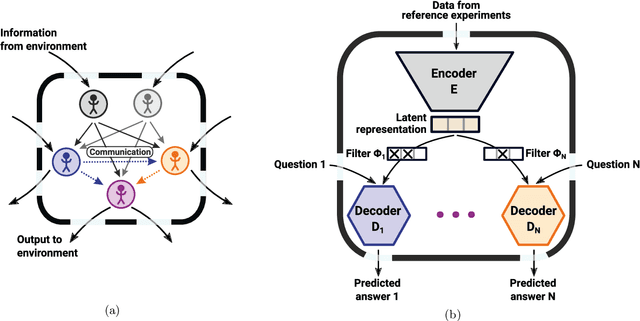
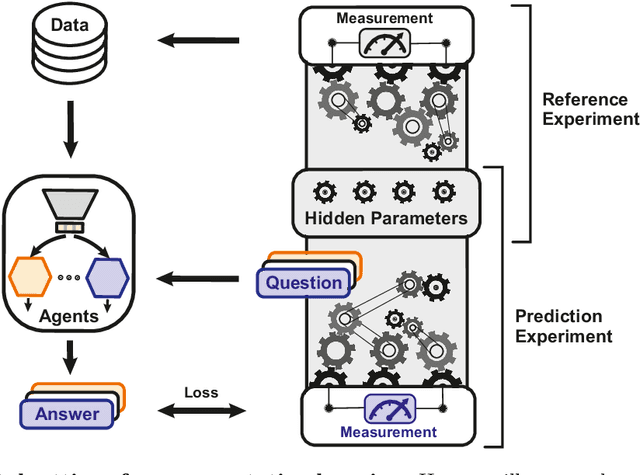
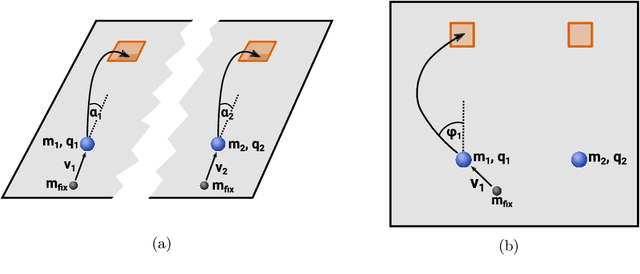
To make progress in science, we often build abstract representations of physical systems that meaningfully encode information about the systems. The representations learnt by most current machine learning techniques reflect statistical structure present in the training data; however, these methods do not allow us to specify explicit and operationally meaningful requirements on the representation. Here, we present a neural network architecture based on the notion that agents dealing with different aspects of a physical system should be able to communicate relevant information as efficiently as possible to one another. This produces representations that separate different parameters which are useful for making statements about the physical system in different experimental settings. We present examples involving both classical and quantum physics. For instance, our architecture finds a compact representation of an arbitrary two-qubit system that separates local parameters from parameters describing quantum correlations. We further show that this method can be combined with reinforcement learning to enable representation learning within interactive scenarios where agents need to explore experimental settings to identify relevant variables.

A framework for deep energy-based reinforcement learning with quantum speed-up

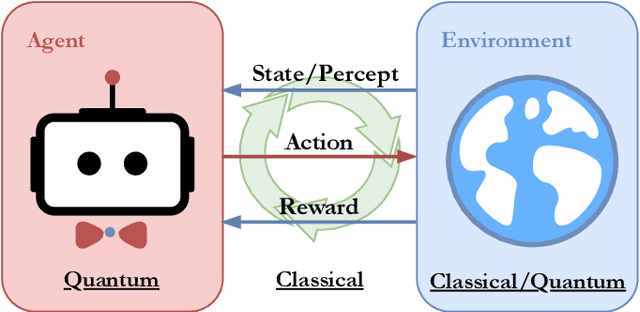
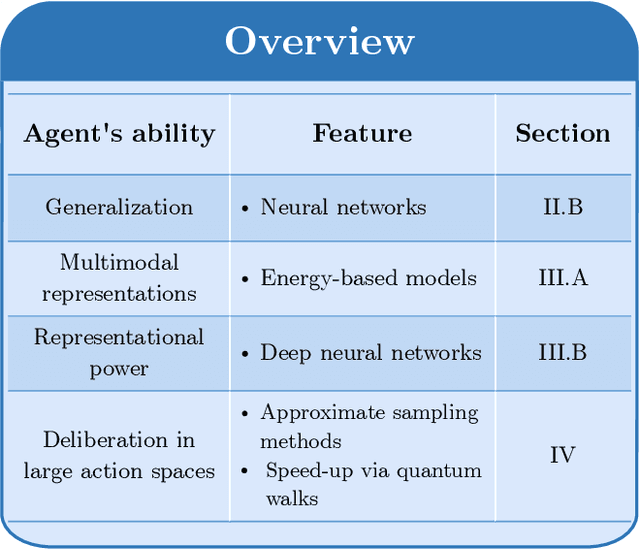
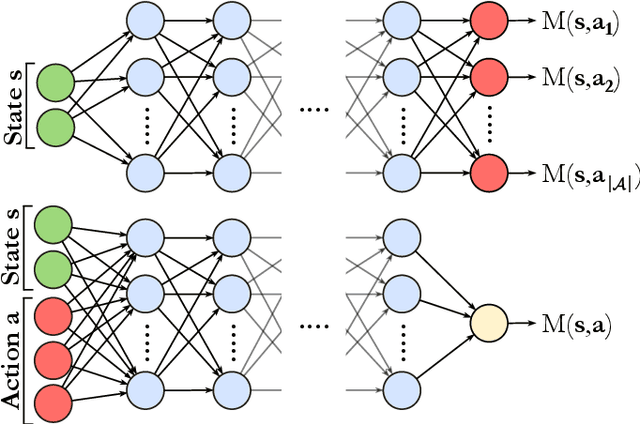
In the past decade, deep learning methods have seen tremendous success in various supervised and unsupervised learning tasks such as classification and generative modeling. More recently, deep neural networks have emerged in the domain of reinforcement learning as a tool to solve decision-making problems of unprecedented complexity, e.g., navigation problems or game-playing AI. Despite the successful combinations of ideas from quantum computing with machine learning methods, there have been relatively few attempts to design quantum algorithms that would enhance deep reinforcement learning. This is partly due to the fact that quantum enhancements of deep neural networks, in general, have not been as extensively investigated as other quantum machine learning methods. In contrast, projective simulation is a reinforcement learning model inspired by the stochastic evolution of physical systems that enables a quantum speed-up in decision making. In this paper, we develop a unifying framework that connects deep learning and projective simulation, opening the route to quantum improvements in deep reinforcement learning. Our approach is based on so-called generative energy-based models to design reinforcement learning methods with a computational advantage in solving complex and large-scale decision-making problems.

On the convergence of projective-simulation-based reinforcement learning in Markov decision processes

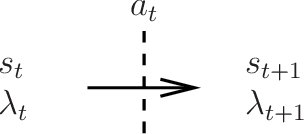
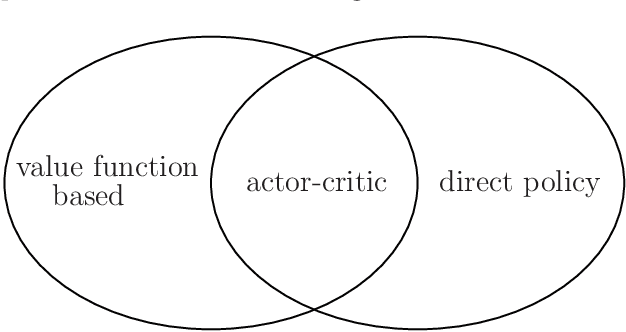
In recent years, the interest in leveraging quantum effects for enhancing machine learning tasks has significantly increased. Many algorithms speeding up supervised and unsupervised learning were established. The first framework in which ways to exploit quantum resources specifically for the broader context of reinforcement learning were found is projective simulation. Projective simulation presents an agent-based reinforcement learning approach designed in a manner which may support quantum walk-based speed-ups. Although classical variants of projective simulation have been benchmarked against common reinforcement learning algorithms, very few formal theoretical analyses have been provided for its performance in standard learning scenarios. In this paper, we provide a detailed formal discussion of the properties of this model. Specifically, we prove that one version of the projective simulation model, understood as a reinforcement learning approach, converges to optimal behavior in a large class of Markov decision processes. This proof shows that a physically-inspired approach to reinforcement learning can guarantee to converge.

Photonic architecture for reinforcement learning

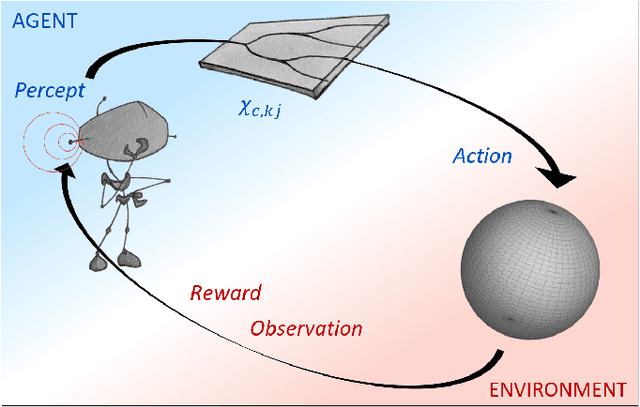
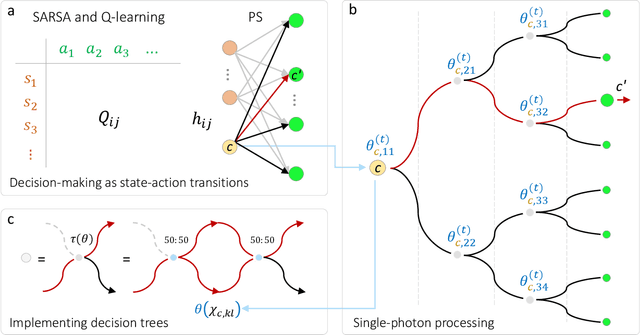
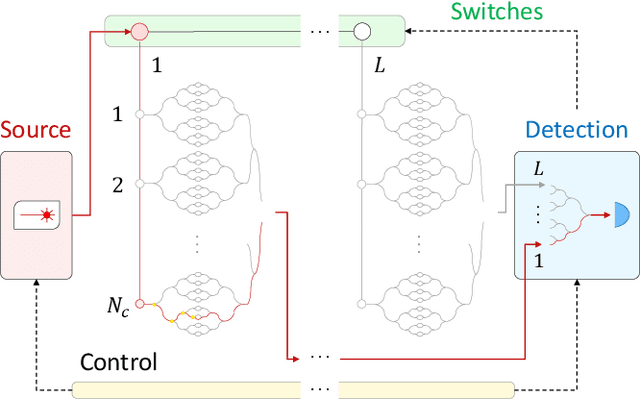
The last decade has seen an unprecedented growth in artificial intelligence and photonic technologies, both of which drive the limits of modern-day computing devices. In line with these recent developments, this work brings together the state of the art of both fields within the framework of reinforcement learning. We present the blueprint for a photonic implementation of an active learning machine incorporating contemporary algorithms such as SARSA, Q-learning, and projective simulation. We numerically investigate its performance within typical reinforcement learning environments, showing that realistic levels of experimental noise can be tolerated or even be beneficial for the learning process. Remarkably, the architecture itself enables mechanisms of abstraction and generalization, two features which are often considered key ingredients for artificial intelligence. The proposed architecture, based on single-photon evolution on a mesh of tunable beamsplitters, is simple, scalable, and a first integration in portable systems appears to be within the reach of near-term technology.