Reinforcement learning for optimization of variational quantum circuit architectures
Paper and Code
Mar 30, 2021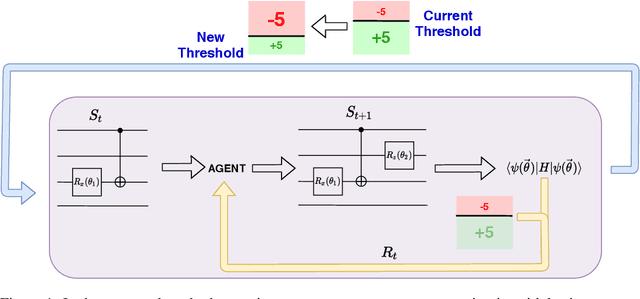

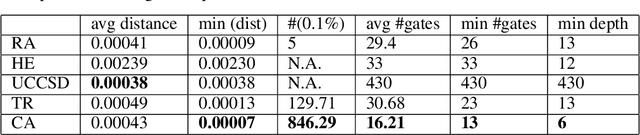
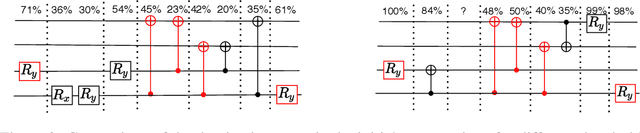
The study of Variational Quantum Eigensolvers (VQEs) has been in the spotlight in recent times as they may lead to real-world applications of near-term quantum devices. However, their performance depends on the structure of the used variational ansatz, which requires balancing the depth and expressivity of the corresponding circuit. In recent years, various methods for VQE structure optimization have been introduced but the capacities of machine learning to aid with this problem has not yet been fully investigated. In this work, we propose a reinforcement learning algorithm that autonomously explores the space of possible ans{\"a}tze, identifying economic circuits which still yield accurate ground energy estimates. The algorithm is intrinsically motivated, and it incrementally improves the accuracy of the result while minimizing the circuit depth. We showcase the performance of our algorithm on the problem of estimating the ground-state energy of lithium hydride (LiH). In this well-known benchmark problem, we achieve chemical accuracy, as well as state-of-the-art results in terms of circuit depth.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge