Interpretable Machine Learning in Physics: A Review

Machine learning is increasingly transforming various scientific fields, enabled by advancements in computational power and access to large data sets from experiments and simulations. As artificial intelligence (AI) continues to grow in capability, these algorithms will enable many scientific discoveries beyond human capabilities. Since the primary goal of science is to understand the world around us, fully leveraging machine learning in scientific discovery requires models that are interpretable -- allowing experts to comprehend the concepts underlying machine-learned predictions. Successful interpretations increase trust in black-box methods, help reduce errors, allow for the improvement of the underlying models, enhance human-AI collaboration, and ultimately enable fully automated scientific discoveries that remain understandable to human scientists. This review examines the role of interpretability in machine learning applied to physics. We categorize different aspects of interpretability, discuss machine learning models in terms of both interpretability and performance, and explore the philosophical implications of interpretability in scientific inquiry. Additionally, we highlight recent advances in interpretable machine learning across many subfields of physics. By bridging boundaries between disciplines -- each with its own unique insights and challenges -- we aim to establish interpretable machine learning as a core research focus in science.

Operationally meaningful representations of physical systems in neural networks

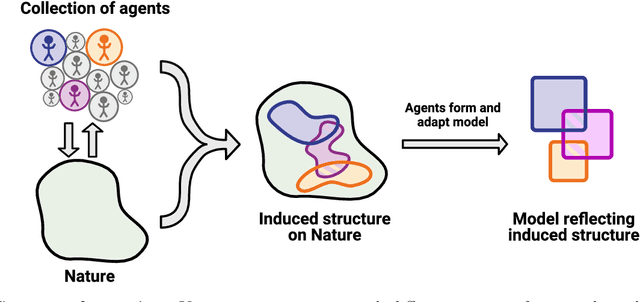
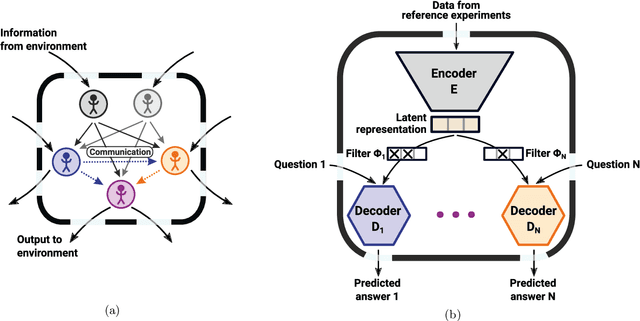
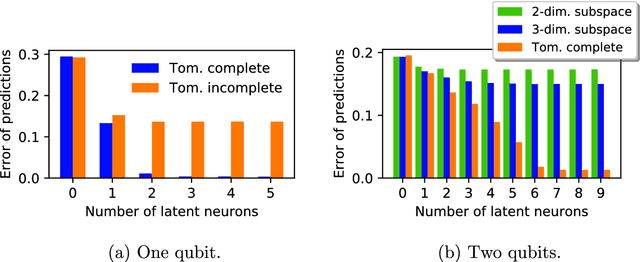
To make progress in science, we often build abstract representations of physical systems that meaningfully encode information about the systems. The representations learnt by most current machine learning techniques reflect statistical structure present in the training data; however, these methods do not allow us to specify explicit and operationally meaningful requirements on the representation. Here, we present a neural network architecture based on the notion that agents dealing with different aspects of a physical system should be able to communicate relevant information as efficiently as possible to one another. This produces representations that separate different parameters which are useful for making statements about the physical system in different experimental settings. We present examples involving both classical and quantum physics. For instance, our architecture finds a compact representation of an arbitrary two-qubit system that separates local parameters from parameters describing quantum correlations. We further show that this method can be combined with reinforcement learning to enable representation learning within interactive scenarios where agents need to explore experimental settings to identify relevant variables.

Discovering physical concepts with neural networks

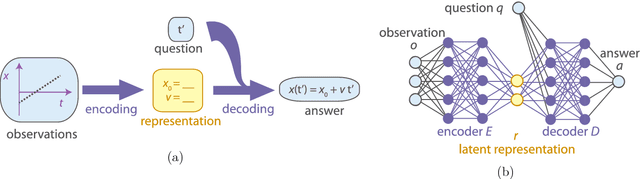
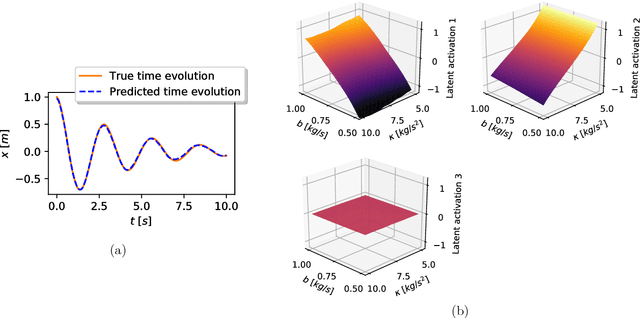
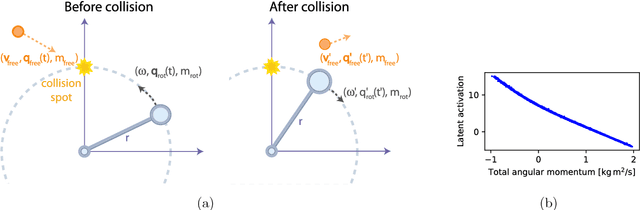
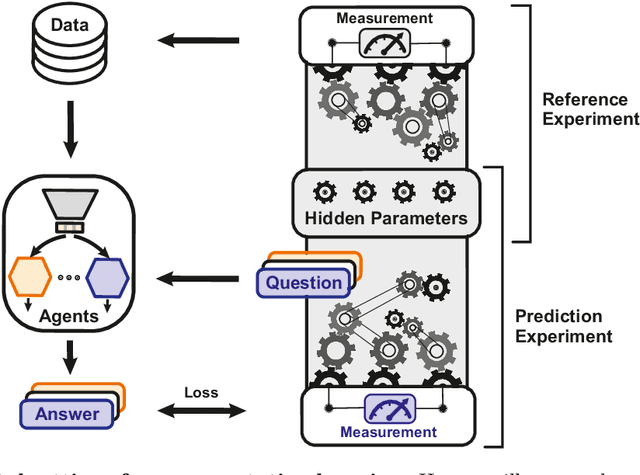
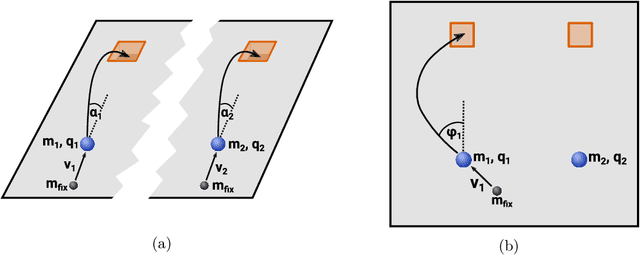
We introduce a neural network architecture that models the physical reasoning process and that can be used to extract simple physical concepts from experimental data without being provided with additional prior knowledge. We apply the neural network to a variety of simple physical examples in classical and quantum mechanics, like damped pendulums, two-particle collisions, and qubits. The network finds the physically relevant parameters, exploits conservation laws to make predictions, and can be used to gain conceptual insights. For example, given a time series of the positions of the Sun and Mars as observed from Earth, the network discovers the heliocentric model of the solar system - that is, it encodes the data into the angles of the two planets as seen from the Sun. Our work provides a first step towards answering the question whether the traditional ways by which physicists model nature naturally arise from the experimental data without any mathematical and physical pre-knowledge, or if there are alternative elegant formalisms, which may solve some of the fundamental conceptual problems in modern physics, such as the measurement problem in quantum mechanics.