Inferring the Langevin Equation with Uncertainty via Bayesian Neural Networks

Pervasive across diverse domains, stochastic systems exhibit fluctuations in processes ranging from molecular dynamics to climate phenomena. The Langevin equation has served as a common mathematical model for studying such systems, enabling predictions of their temporal evolution and analyses of thermodynamic quantities, including absorbed heat, work done on the system, and entropy production. However, inferring the Langevin equation from observed trajectories remains challenging, particularly for nonlinear and high-dimensional systems. In this study, we present a comprehensive framework that employs Bayesian neural networks for inferring Langevin equations in both overdamped and underdamped regimes. Our framework first provides the drift force and diffusion matrix separately and then combines them to construct the Langevin equation. By providing a distribution of predictions instead of a single value, our approach allows us to assess prediction uncertainties, which can prevent potential misunderstandings and erroneous decisions about the system. We demonstrate the effectiveness of our framework in inferring Langevin equations for various scenarios including a neuron model and microscopic engine, highlighting its versatility and potential impact.

Learning Heterogeneous Interaction Strengths by Trajectory Prediction with Graph Neural Network

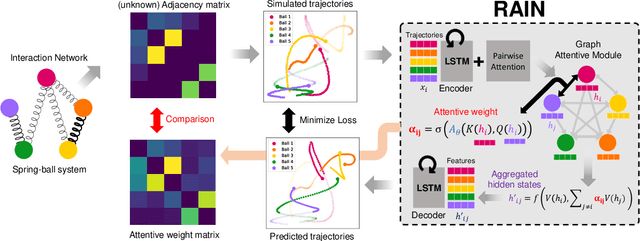
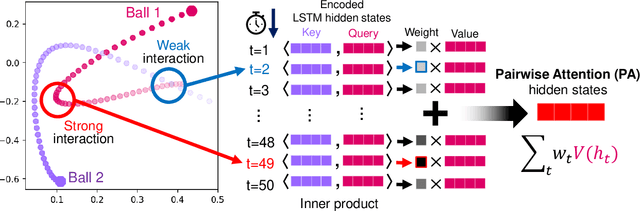
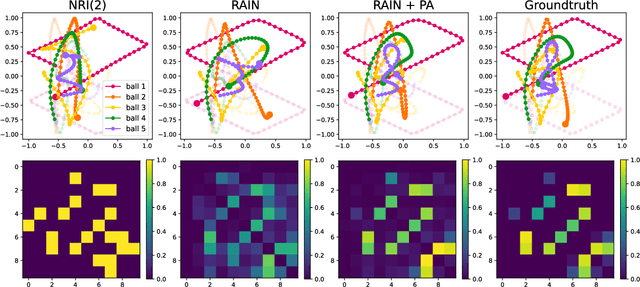
Dynamical systems with interacting agents are universal in nature, commonly modeled by a graph of relationships between their constituents. Recently, various works have been presented to tackle the problem of inferring those relationships from the system trajectories via deep neural networks, but most of the studies assume binary or discrete types of interactions for simplicity. In the real world, the interaction kernels often involve continuous interaction strengths, which cannot be accurately approximated by discrete relations. In this work, we propose the relational attentive inference network (RAIN) to infer continuously weighted interaction graphs without any ground-truth interaction strengths. Our model employs a novel pairwise attention (PA) mechanism to refine the trajectory representations and a graph transformer to extract heterogeneous interaction weights for each pair of agents. We show that our RAIN model with the PA mechanism accurately infers continuous interaction strengths for simulated physical systems in an unsupervised manner. Further, RAIN with PA successfully predicts trajectories from motion capture data with an interpretable interaction graph, demonstrating the virtue of modeling unknown dynamics with continuous weights.

Social learning spontaneously emerges by searching optimal heuristics with deep reinforcement learning

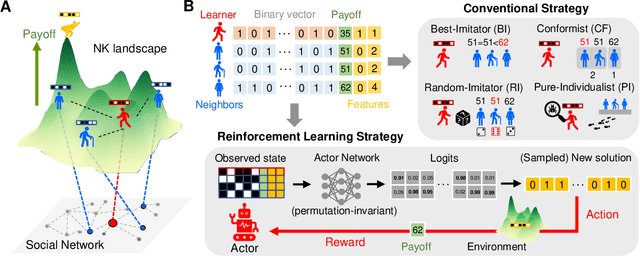
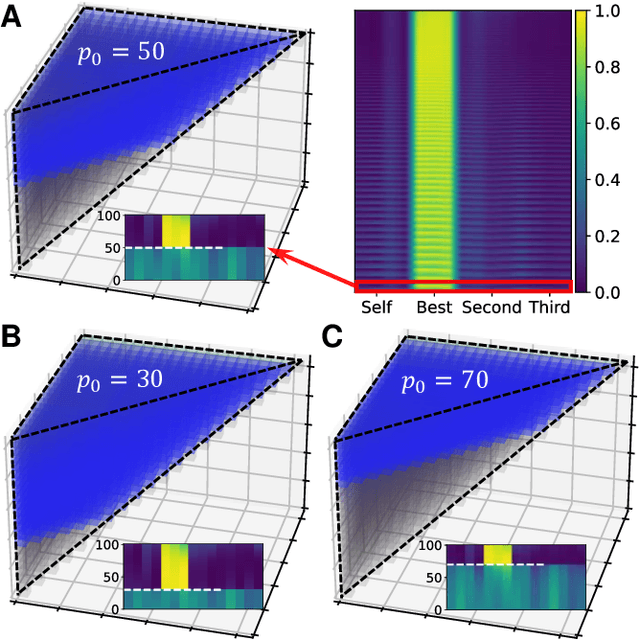
How have individuals of social animals in nature evolved to learn from each other, and what would be the optimal strategy for such learning in a specific environment? Here, we address both problems by employing a deep reinforcement learning model to optimize the social learning strategies (SLSs) of agents in a cooperative game in a multi-dimensional landscape. Throughout the training for maximizing the overall payoff, we find that the agent spontaneously learns various concepts of social learning, such as copying, focusing on frequent and well-performing neighbors, self-comparison, and the importance of balancing between individual and social learning, without any explicit guidance or prior knowledge about the system. The SLS from a fully trained agent outperforms all of the traditional, baseline SLSs in terms of mean payoff. We demonstrate the superior performance of the reinforcement learning agent in various environments, including temporally changing environments and real social networks, which also verifies the adaptability of our framework to different social settings.

Discovering conservation laws from trajectories via machine learning

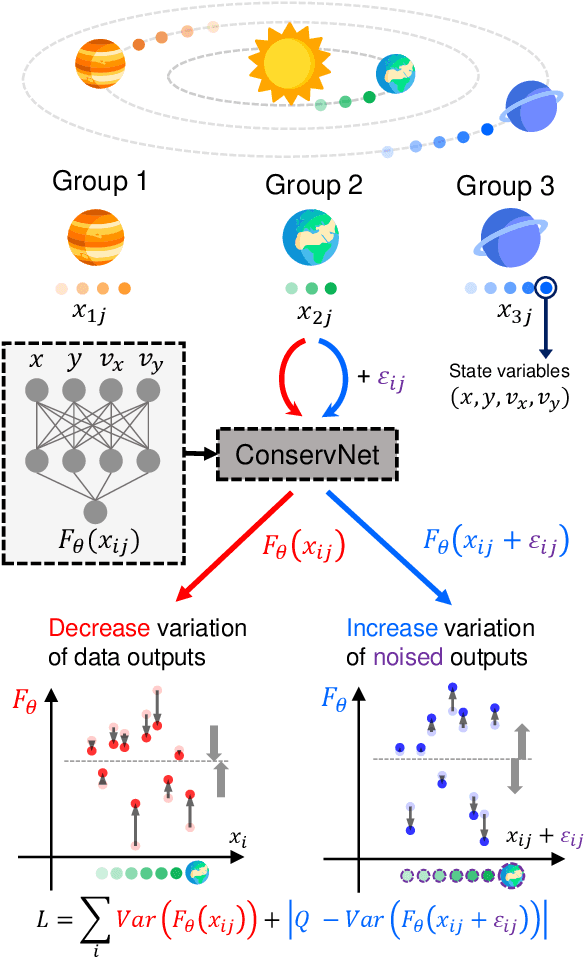
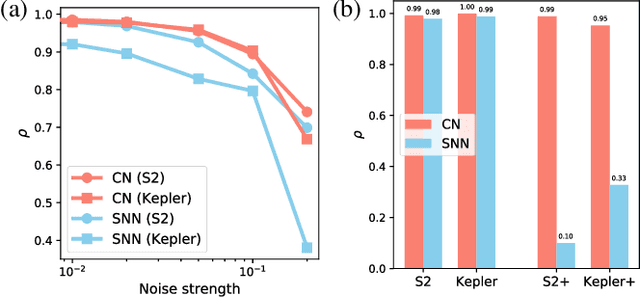
Invariants and conservation laws convey critical information about the underlying dynamics of a system, yet it is generally infeasible to find them without any prior knowledge. We propose ConservNet to achieve this goal, a neural network that extracts a conserved quantity from grouped data where the members of each group share invariants. As a neural network trained with a novel and intuitive loss function called noise-variance loss, ConservNet learns the hidden invariants in each group of multi-dimensional observables in a data-driven, end-to-end manner. We demonstrate the capability of our model with simulated systems having invariants as well as a real-world double pendulum trajectory. ConservNet successfully discovers underlying invariants from the systems from a small number of data points, namely less than several thousand. Since the model is robust to noise and data conditions compared to baseline, our approach is directly applicable to experimental data for discovering hidden conservation laws and relationships between variables.

Towards Automated Statistical Physics : Data-driven Modeling of Complex Systems with Deep Learning

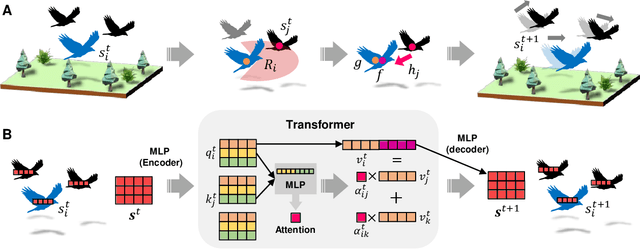
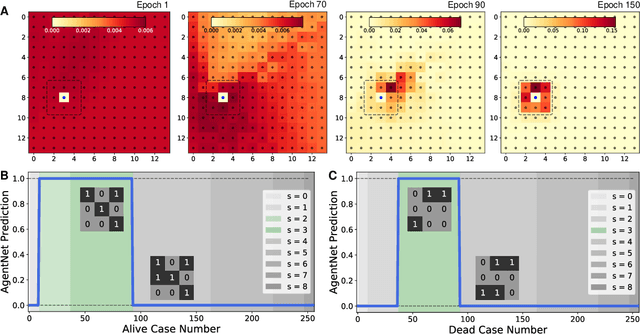
Rich phenomena from complex systems have long intrigued researchers, and yet modeling system micro-dynamics and inferring the forms of interaction are challenging for conventional data-driven approaches, being generally established by human scientists. In this study, we propose AgentNet, a generalized data-driven framework to analyze and understand the hidden interactions in complex systems. AgentNet utilizes a graph attention network to model the interaction between individual agents and employs various encoders and decoders that can be selectively applied to any desired system. Our model successfully captured three different simulated complex systems, namely cellular automata, the Vicsek model, and active Ornstein-Uhlenbeck particles in which, notably, AgentNet's visualized attention values coincided with the true interaction strength. Demonstration with empirical data from a flock of birds showed that AgentNet prediction could yield the qualitatively same collective phenomena as exhibited by real birds. We expect our framework to open a novel path to investigating complex systems and to provide insight into process-driven modeling.