Discovering conservation laws from trajectories via machine learning
Paper and Code
Feb 08, 2021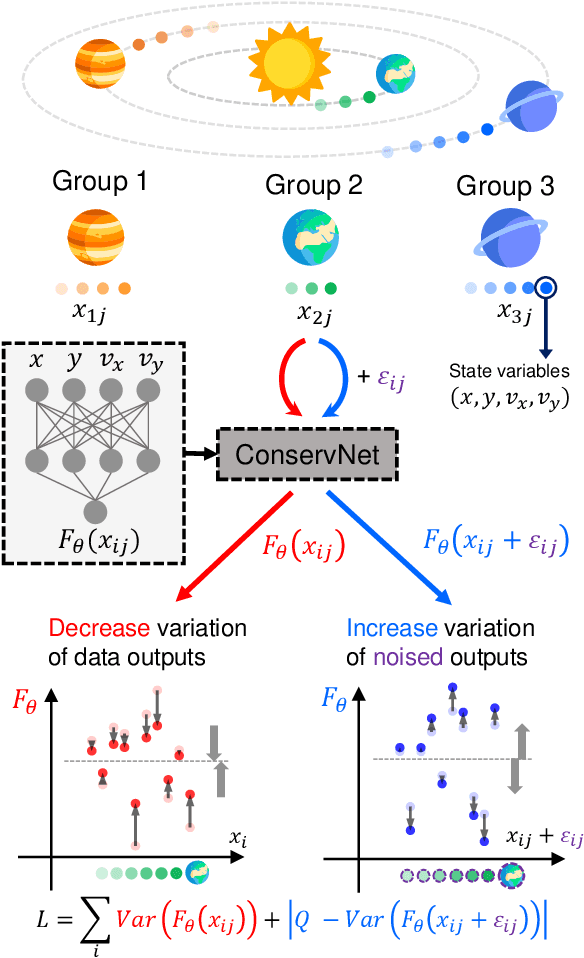

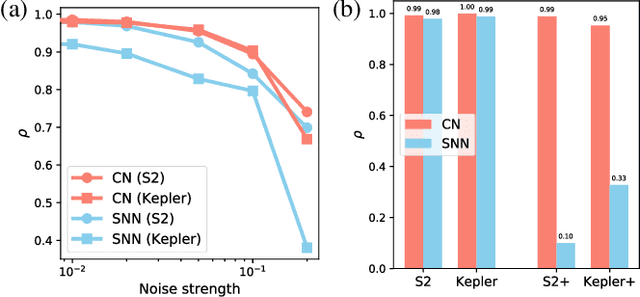

Invariants and conservation laws convey critical information about the underlying dynamics of a system, yet it is generally infeasible to find them without any prior knowledge. We propose ConservNet to achieve this goal, a neural network that extracts a conserved quantity from grouped data where the members of each group share invariants. As a neural network trained with a novel and intuitive loss function called noise-variance loss, ConservNet learns the hidden invariants in each group of multi-dimensional observables in a data-driven, end-to-end manner. We demonstrate the capability of our model with simulated systems having invariants as well as a real-world double pendulum trajectory. ConservNet successfully discovers underlying invariants from the systems from a small number of data points, namely less than several thousand. Since the model is robust to noise and data conditions compared to baseline, our approach is directly applicable to experimental data for discovering hidden conservation laws and relationships between variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge