Exploring how deep learning decodes anomalous diffusion via Grad-CAM

While deep learning has been successfully applied to the data-driven classification of anomalous diffusion mechanisms, how the algorithm achieves the feat still remains a mystery. In this study, we use a well-known technique aimed at achieving explainable AI, namely the Gradient-weighted Class Activation Map (Grad-CAM), to investigate how deep learning (implemented by ResNets) recognizes the distinctive features of a particular anomalous diffusion model from the raw trajectory data. Our results show that Grad-CAM reveals the portions of the trajectory that hold crucial information about the underlying mechanism of anomalous diffusion, which can be utilized to enhance the robustness of the trained classifier against the measurement noise. Moreover, we observe that deep learning distills unique statistical characteristics of different diffusion mechanisms at various spatiotemporal scales, with larger-scale (smaller-scale) features identified at higher (lower) layers.

Stochastic Restarting to Overcome Overfitting in Neural Networks with Noisy Labels

Despite its prevalence, giving up and starting over may seem wasteful in many situations such as searching for a target or training deep neural networks (DNNs). Our study, though, demonstrates that restarting from a checkpoint can significantly improve generalization performance when training DNNs with noisy labels. In the presence of noisy labels, DNNs initially learn the general patterns of the data but then gradually overfit to the noisy labels. To combat this overfitting phenomenon, we developed a method based on stochastic restarting, which has been actively explored in the statistical physics field for finding targets efficiently. By approximating the dynamics of stochastic gradient descent into Langevin dynamics, we theoretically show that restarting can provide great improvements as the batch size and the proportion of corrupted data increase. We then empirically validate our theory, confirming the significant improvements achieved by restarting. An important aspect of our method is its ease of implementation and compatibility with other methods, while still yielding notably improved performance. We envision it as a valuable tool that can complement existing methods for handling noisy labels.

From Empirical Observations to Universality: Dynamics of Deep Learning with Inputs Built on Gaussian mixture

This study broadens the scope of theoretical frameworks in deep learning by delving into the dynamics of neural networks with inputs that demonstrate the structural characteristics to Gaussian Mixture (GM). We analyzed how the dynamics of neural networks under GM-structured inputs diverge from the predictions of conventional theories based on simple Gaussian structures. A revelation of our work is the observed convergence of neural network dynamics towards conventional theory even with standardized GM inputs, highlighting an unexpected universality. We found that standardization, especially in conjunction with certain nonlinear functions, plays a critical role in this phenomena. Consequently, despite the complex and varied nature of GM distributions, we demonstrate that neural networks exhibit asymptotic behaviors in line with predictions under simple Gaussian frameworks.

Inferring the Langevin Equation with Uncertainty via Bayesian Neural Networks

Pervasive across diverse domains, stochastic systems exhibit fluctuations in processes ranging from molecular dynamics to climate phenomena. The Langevin equation has served as a common mathematical model for studying such systems, enabling predictions of their temporal evolution and analyses of thermodynamic quantities, including absorbed heat, work done on the system, and entropy production. However, inferring the Langevin equation from observed trajectories remains challenging, particularly for nonlinear and high-dimensional systems. In this study, we present a comprehensive framework that employs Bayesian neural networks for inferring Langevin equations in both overdamped and underdamped regimes. Our framework first provides the drift force and diffusion matrix separately and then combines them to construct the Langevin equation. By providing a distribution of predictions instead of a single value, our approach allows us to assess prediction uncertainties, which can prevent potential misunderstandings and erroneous decisions about the system. We demonstrate the effectiveness of our framework in inferring Langevin equations for various scenarios including a neuron model and microscopic engine, highlighting its versatility and potential impact.

Identifying Hamiltonian manifold in neural networks

Recent studies to learn physical laws via deep learning attempt to find the shared representation of the given system by introducing physics priors or inductive biases to the neural network. However, most of these approaches tackle the problem in a system-specific manner, in which one neural network trained to one particular physical system cannot be easily adapted to another system governed by a different physical law. In this work, we use a meta-learning algorithm to identify the general manifold in neural networks that represents Hamilton's equation. We meta-trained the model with the dataset composed of five dynamical systems each governed by different physical laws. We show that with only a few gradient steps, the meta-trained model adapts well to the physical system which was unseen during the meta-training phase. Our results suggest that the meta-trained model can craft the representation of Hamilton's equation in neural networks which is shared across various dynamical systems with each governed by different physical laws.

Learning Heterogeneous Interaction Strengths by Trajectory Prediction with Graph Neural Network

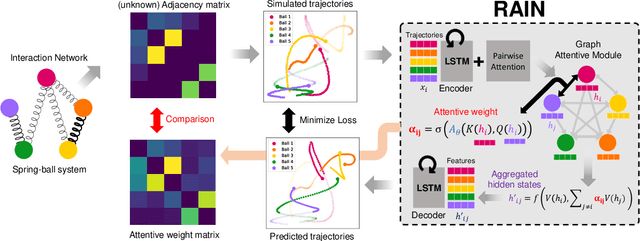
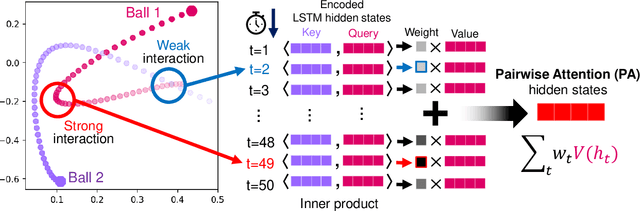
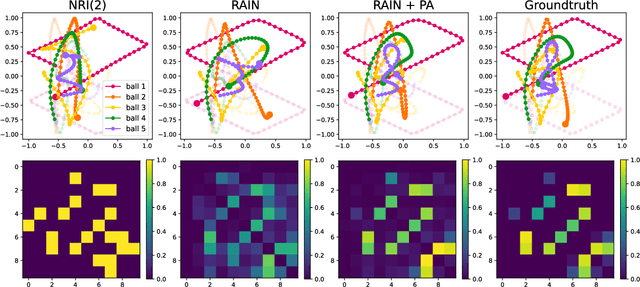
Dynamical systems with interacting agents are universal in nature, commonly modeled by a graph of relationships between their constituents. Recently, various works have been presented to tackle the problem of inferring those relationships from the system trajectories via deep neural networks, but most of the studies assume binary or discrete types of interactions for simplicity. In the real world, the interaction kernels often involve continuous interaction strengths, which cannot be accurately approximated by discrete relations. In this work, we propose the relational attentive inference network (RAIN) to infer continuously weighted interaction graphs without any ground-truth interaction strengths. Our model employs a novel pairwise attention (PA) mechanism to refine the trajectory representations and a graph transformer to extract heterogeneous interaction weights for each pair of agents. We show that our RAIN model with the PA mechanism accurately infers continuous interaction strengths for simulated physical systems in an unsupervised manner. Further, RAIN with PA successfully predicts trajectories from motion capture data with an interpretable interaction graph, demonstrating the virtue of modeling unknown dynamics with continuous weights.

Social learning spontaneously emerges by searching optimal heuristics with deep reinforcement learning

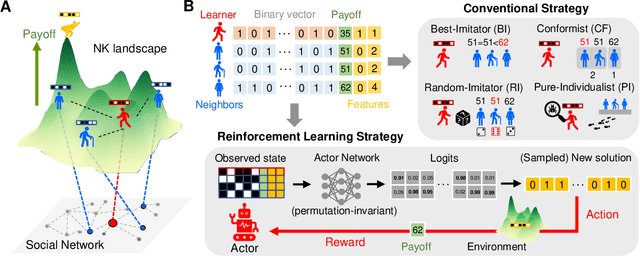
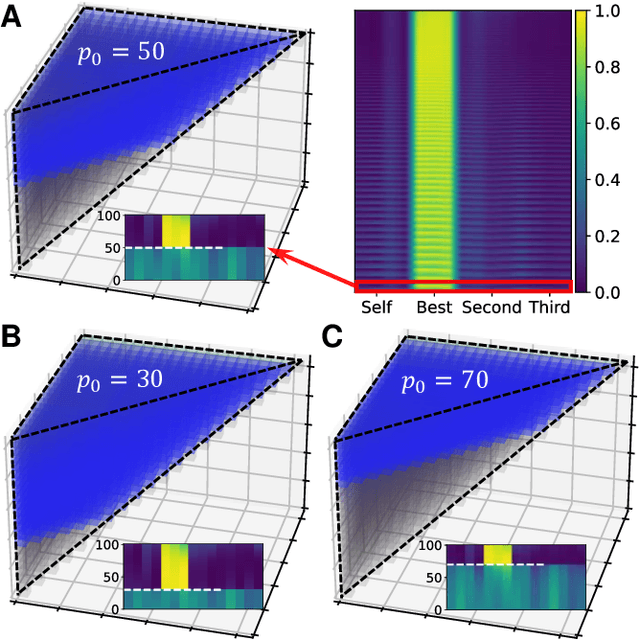
How have individuals of social animals in nature evolved to learn from each other, and what would be the optimal strategy for such learning in a specific environment? Here, we address both problems by employing a deep reinforcement learning model to optimize the social learning strategies (SLSs) of agents in a cooperative game in a multi-dimensional landscape. Throughout the training for maximizing the overall payoff, we find that the agent spontaneously learns various concepts of social learning, such as copying, focusing on frequent and well-performing neighbors, self-comparison, and the importance of balancing between individual and social learning, without any explicit guidance or prior knowledge about the system. The SLS from a fully trained agent outperforms all of the traditional, baseline SLSs in terms of mean payoff. We demonstrate the superior performance of the reinforcement learning agent in various environments, including temporally changing environments and real social networks, which also verifies the adaptability of our framework to different social settings.

Attaining entropy production and dissipation maps from Brownian movies via neural networks

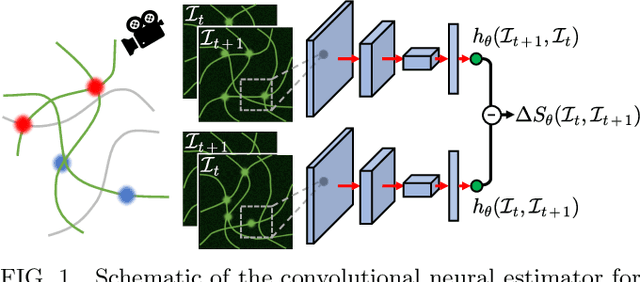
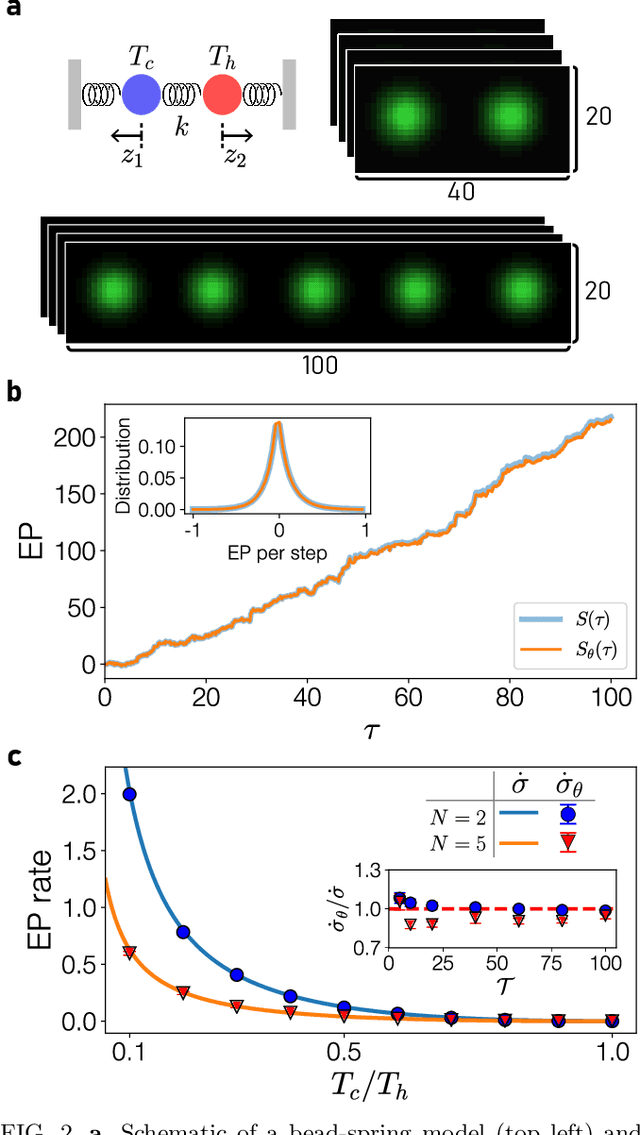
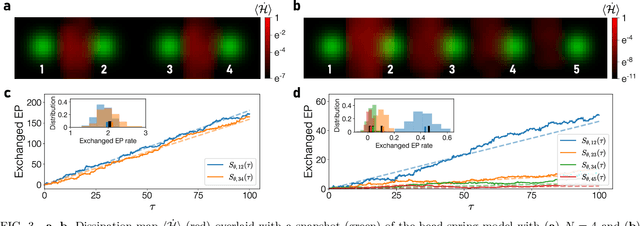
Quantifying entropy production (EP) is essential to understand stochastic systems at mesoscopic scales, such as living organisms or biological assemblies. However, without tracking the relevant variables, it is challenging to figure out where and to what extent EP occurs from recorded time-series image data from experiments. Here, applying a convolutional neural network (CNN), a powerful tool for image processing, we develop an estimation method for EP through an unsupervised learning algorithm that calculates only from movies. Together with an attention map of the CNN's last layer, our method can not only quantify stochastic EP but also produce the spatiotemporal pattern of the EP (dissipation map). We show that our method accurately measures the EP and creates a dissipation map in two nonequilibrium systems, the bead-spring model and a network of elastic filaments. We further confirm high performance even with noisy, low spatial resolution data, and partially observed situations. Our method will provide a practical way to obtain dissipation maps and ultimately contribute to uncovering the nonequilibrium nature of complex systems.

Discovering conservation laws from trajectories via machine learning

Invariants and conservation laws convey critical information about the underlying dynamics of a system, yet it is generally infeasible to find them without any prior knowledge. We propose ConservNet to achieve this goal, a neural network that extracts a conserved quantity from grouped data where the members of each group share invariants. As a neural network trained with a novel and intuitive loss function called noise-variance loss, ConservNet learns the hidden invariants in each group of multi-dimensional observables in a data-driven, end-to-end manner. We demonstrate the capability of our model with simulated systems having invariants as well as a real-world double pendulum trajectory. ConservNet successfully discovers underlying invariants from the systems from a small number of data points, namely less than several thousand. Since the model is robust to noise and data conditions compared to baseline, our approach is directly applicable to experimental data for discovering hidden conservation laws and relationships between variables.

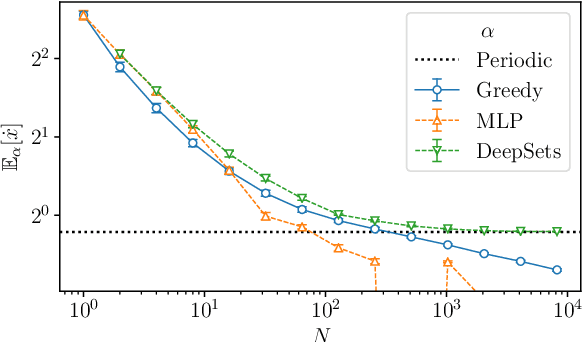
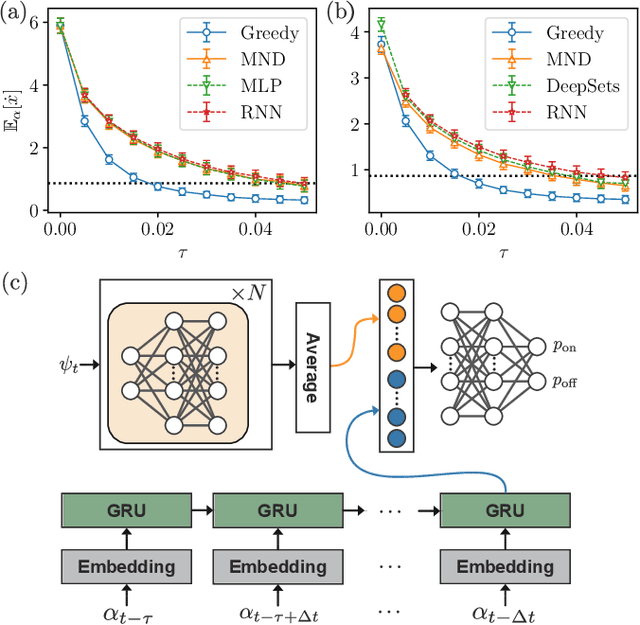
Deep Reinforcement Learning for Feedback Control in a Collective Flashing Ratchet

A collective flashing ratchet transports Brownian particles using a spatially periodic, asymmetric, and time-dependent on-off switchable potential. The net current of the particles in this system can be substantially increased by feedback control based on the particle positions. Several feedback policies for maximizing the current have been proposed, but optimal policies have not been found for a moderate number of particles. Here, we use deep reinforcement learning (RL) to find optimal policies, with results showing that policies built with a suitable neural network architecture outperform the previous policies. Moreover, even in a time-delayed feedback situation where the on-off switching of the potential is delayed, we demonstrate that the policies provided by deep RL provide higher currents than the previous strategies.