Bilinear relational structure fixes reversal curse and enables consistent model editing

The reversal curse -- a language model's (LM) inability to infer an unseen fact ``B is A'' from a learned fact ``A is B'' -- is widely considered a fundamental limitation. We show that this is not an inherent failure but an artifact of how models encode knowledge. By training LMs from scratch on a synthetic dataset of relational knowledge graphs, we demonstrate that bilinear relational structure emerges in their hidden representations. This structure substantially alleviates the reversal curse, enabling LMs to infer unseen reverse facts. Crucially, we also find that this bilinear structure plays a key role in consistent model editing. When a fact is updated in a LM with this structure, the edit correctly propagates to its reverse and other logically dependent facts. In contrast, models lacking this representation not only suffer from the reversal curse but also fail to generalize edits, further introducing logical inconsistencies. Our results establish that training on a relational knowledge dataset induces the emergence of bilinear internal representations, which in turn enable LMs to behave in a logically consistent manner after editing. This implies that the success of model editing depends critically not just on editing algorithms but on the underlying representational geometry of the knowledge being modified.

Erase or Hide? Suppressing Spurious Unlearning Neurons for Robust Unlearning

Large language models trained on web-scale data can memorize private or sensitive knowledge, raising significant privacy risks. Although some unlearning methods mitigate these risks, they remain vulnerable to "relearning" during subsequent training, allowing a substantial portion of forgotten knowledge to resurface. In this paper, we show that widely used unlearning methods cause shallow alignment: instead of faithfully erasing target knowledge, they generate spurious unlearning neurons that amplify negative influence to hide it. To overcome this limitation, we introduce Ssiuu, a new class of unlearning methods that employs attribution-guided regularization to prevent spurious negative influence and faithfully remove target knowledge. Experimental results confirm that our method reliably erases target knowledge and outperforms strong baselines across two practical retraining scenarios: (1) adversarial injection of private data, and (2) benign attack using an instruction-following benchmark. Our findings highlight the necessity of robust and faithful unlearning methods for safe deployment of language models.

Uncovering Emergent Physics Representations Learned In-Context by Large Language Models

Large language models (LLMs) exhibit impressive in-context learning (ICL) abilities, enabling them to solve wide range of tasks via textual prompts alone. As these capabilities advance, the range of applicable domains continues to expand significantly. However, identifying the precise mechanisms or internal structures within LLMs that allow successful ICL across diverse, distinct classes of tasks remains elusive. Physics-based tasks offer a promising testbed for probing this challenge. Unlike synthetic sequences such as basic arithmetic or symbolic equations, physical systems provide experimentally controllable, real-world data based on structured dynamics grounded in fundamental principles. This makes them particularly suitable for studying the emergent reasoning behaviors of LLMs in a realistic yet tractable setting. Here, we mechanistically investigate the ICL ability of LLMs, especially focusing on their ability to reason about physics. Using a dynamics forecasting task in physical systems as a proxy, we evaluate whether LLMs can learn physics in context. We first show that the performance of dynamics forecasting in context improves with longer input contexts. To uncover how such capability emerges in LLMs, we analyze the model's residual stream activations using sparse autoencoders (SAEs). Our experiments reveal that the features captured by SAEs correlate with key physical variables, such as energy. These findings demonstrate that meaningful physical concepts are encoded within LLMs during in-context learning. In sum, our work provides a novel case study that broadens our understanding of how LLMs learn in context.

Attaining entropy production and dissipation maps from Brownian movies via neural networks

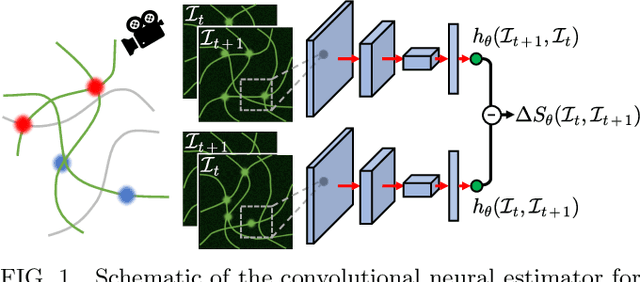
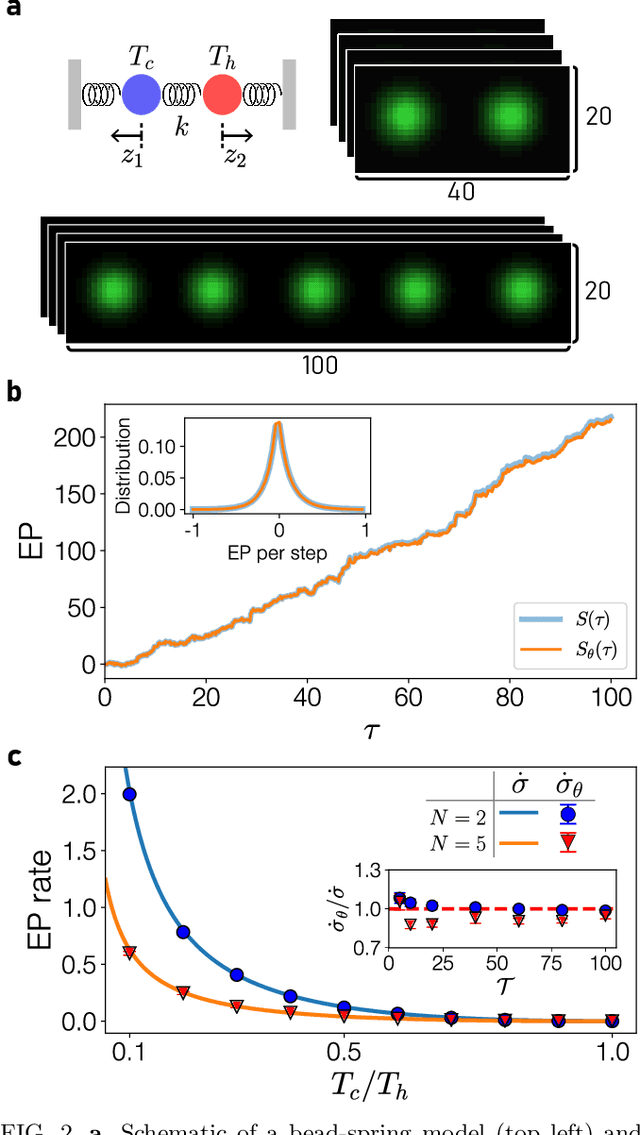
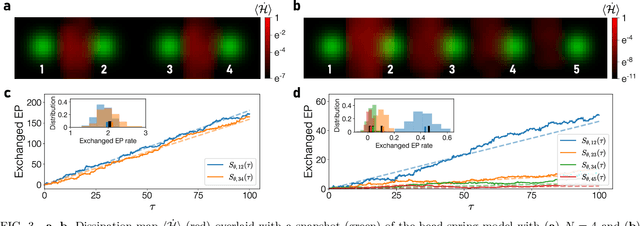
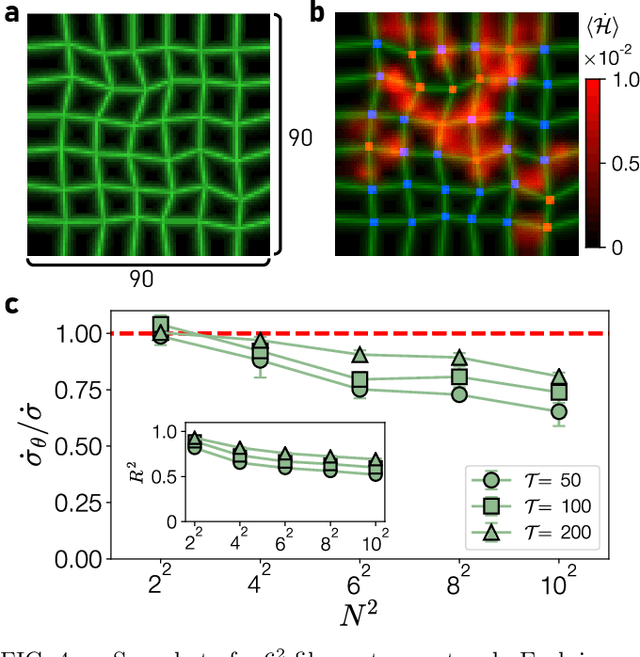
Quantifying entropy production (EP) is essential to understand stochastic systems at mesoscopic scales, such as living organisms or biological assemblies. However, without tracking the relevant variables, it is challenging to figure out where and to what extent EP occurs from recorded time-series image data from experiments. Here, applying a convolutional neural network (CNN), a powerful tool for image processing, we develop an estimation method for EP through an unsupervised learning algorithm that calculates only from movies. Together with an attention map of the CNN's last layer, our method can not only quantify stochastic EP but also produce the spatiotemporal pattern of the EP (dissipation map). We show that our method accurately measures the EP and creates a dissipation map in two nonequilibrium systems, the bead-spring model and a network of elastic filaments. We further confirm high performance even with noisy, low spatial resolution data, and partially observed situations. Our method will provide a practical way to obtain dissipation maps and ultimately contribute to uncovering the nonequilibrium nature of complex systems.

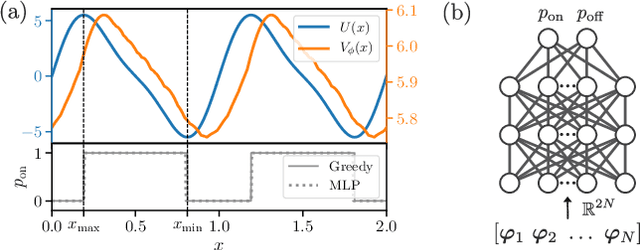
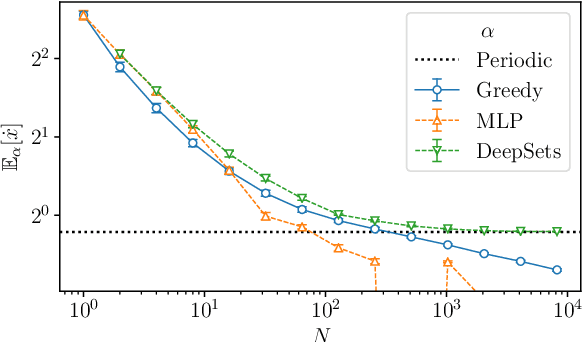
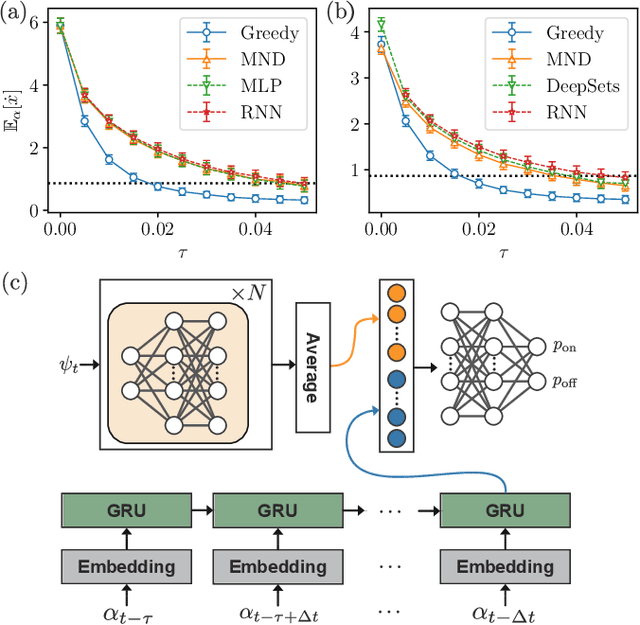
Deep Reinforcement Learning for Feedback Control in a Collective Flashing Ratchet

A collective flashing ratchet transports Brownian particles using a spatially periodic, asymmetric, and time-dependent on-off switchable potential. The net current of the particles in this system can be substantially increased by feedback control based on the particle positions. Several feedback policies for maximizing the current have been proposed, but optimal policies have not been found for a moderate number of particles. Here, we use deep reinforcement learning (RL) to find optimal policies, with results showing that policies built with a suitable neural network architecture outperform the previous policies. Moreover, even in a time-delayed feedback situation where the on-off switching of the potential is delayed, we demonstrate that the policies provided by deep RL provide higher currents than the previous strategies.

Learning entropy production via neural networks

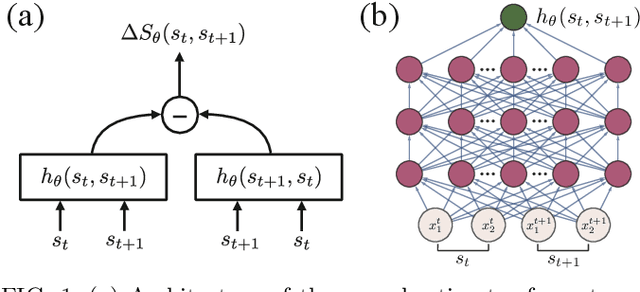
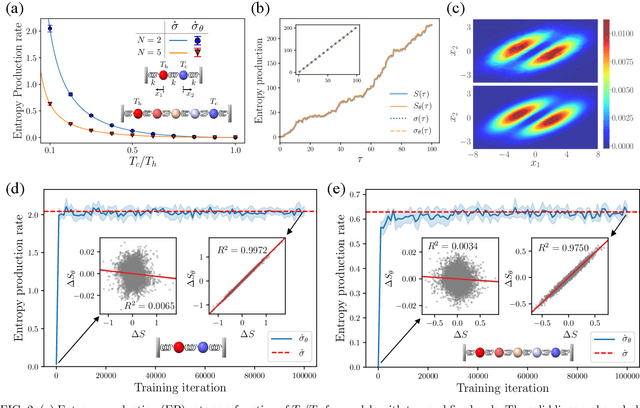
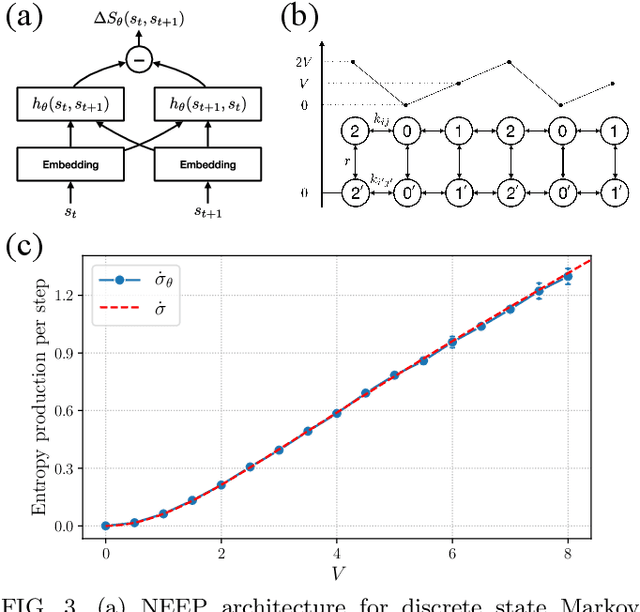
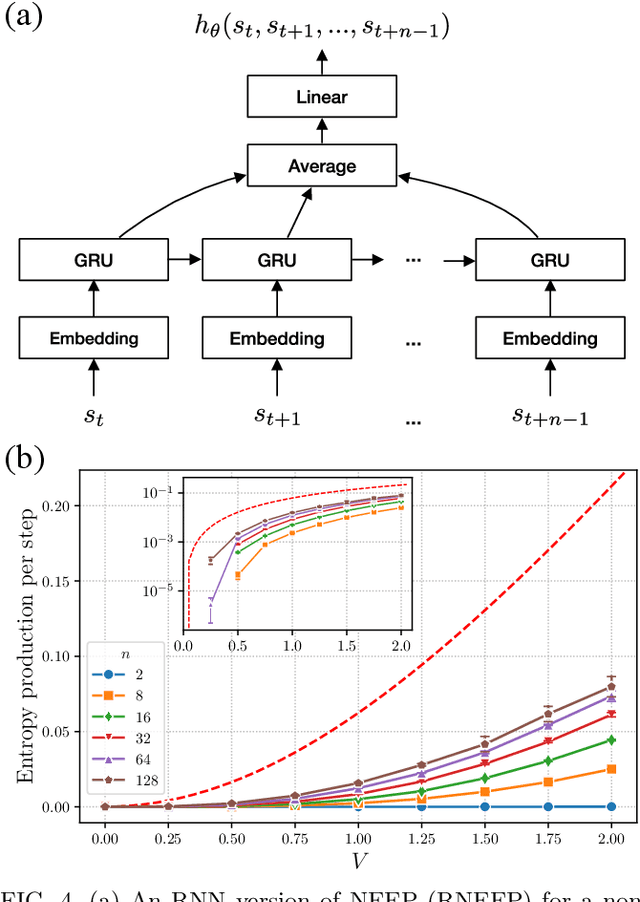
This Letter presents a neural estimator for entropy production, or NEEP, that estimates entropy production (EP) from trajectories without any prior knowledge of the system. For steady state, we rigorously prove that the estimator, which can be built up from different choices of deep neural networks, provides stochastic EP by optimizing the objective function proposed here. We verify the NEEP with the stochastic processes of the bead-spring and discrete flashing ratchet models, and also demonstrate that our method is applicable to high-dimensional data and non-Markovian systems.