Stochastic Restarting to Overcome Overfitting in Neural Networks with Noisy Labels

Despite its prevalence, giving up and starting over may seem wasteful in many situations such as searching for a target or training deep neural networks (DNNs). Our study, though, demonstrates that restarting from a checkpoint can significantly improve generalization performance when training DNNs with noisy labels. In the presence of noisy labels, DNNs initially learn the general patterns of the data but then gradually overfit to the noisy labels. To combat this overfitting phenomenon, we developed a method based on stochastic restarting, which has been actively explored in the statistical physics field for finding targets efficiently. By approximating the dynamics of stochastic gradient descent into Langevin dynamics, we theoretically show that restarting can provide great improvements as the batch size and the proportion of corrupted data increase. We then empirically validate our theory, confirming the significant improvements achieved by restarting. An important aspect of our method is its ease of implementation and compatibility with other methods, while still yielding notably improved performance. We envision it as a valuable tool that can complement existing methods for handling noisy labels.

Inferring the Langevin Equation with Uncertainty via Bayesian Neural Networks

Pervasive across diverse domains, stochastic systems exhibit fluctuations in processes ranging from molecular dynamics to climate phenomena. The Langevin equation has served as a common mathematical model for studying such systems, enabling predictions of their temporal evolution and analyses of thermodynamic quantities, including absorbed heat, work done on the system, and entropy production. However, inferring the Langevin equation from observed trajectories remains challenging, particularly for nonlinear and high-dimensional systems. In this study, we present a comprehensive framework that employs Bayesian neural networks for inferring Langevin equations in both overdamped and underdamped regimes. Our framework first provides the drift force and diffusion matrix separately and then combines them to construct the Langevin equation. By providing a distribution of predictions instead of a single value, our approach allows us to assess prediction uncertainties, which can prevent potential misunderstandings and erroneous decisions about the system. We demonstrate the effectiveness of our framework in inferring Langevin equations for various scenarios including a neuron model and microscopic engine, highlighting its versatility and potential impact.

Attaining entropy production and dissipation maps from Brownian movies via neural networks

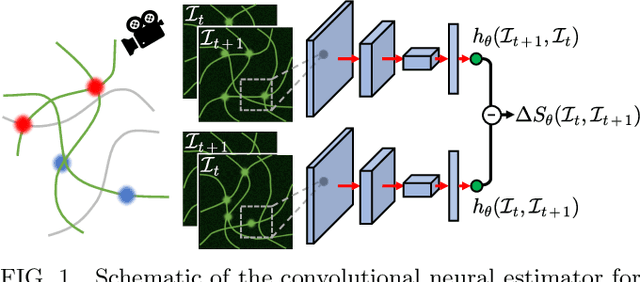
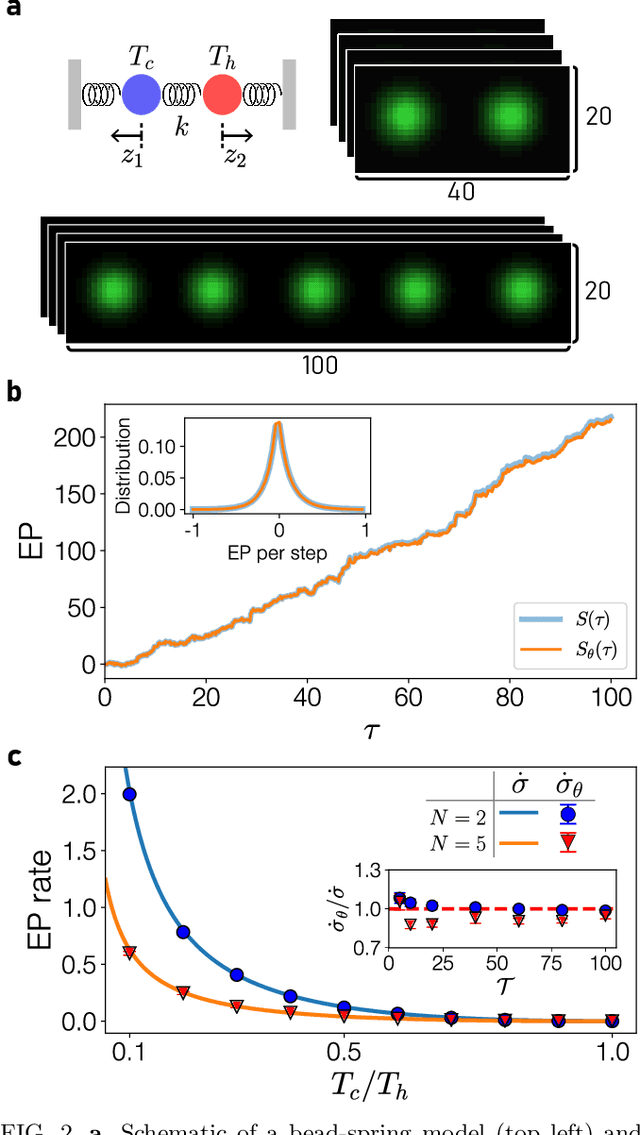
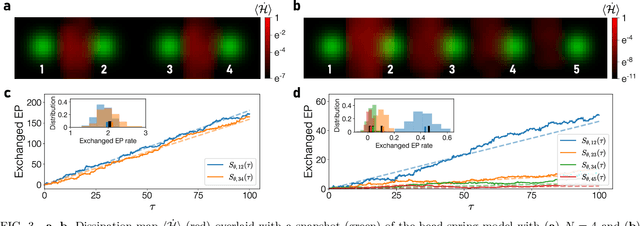
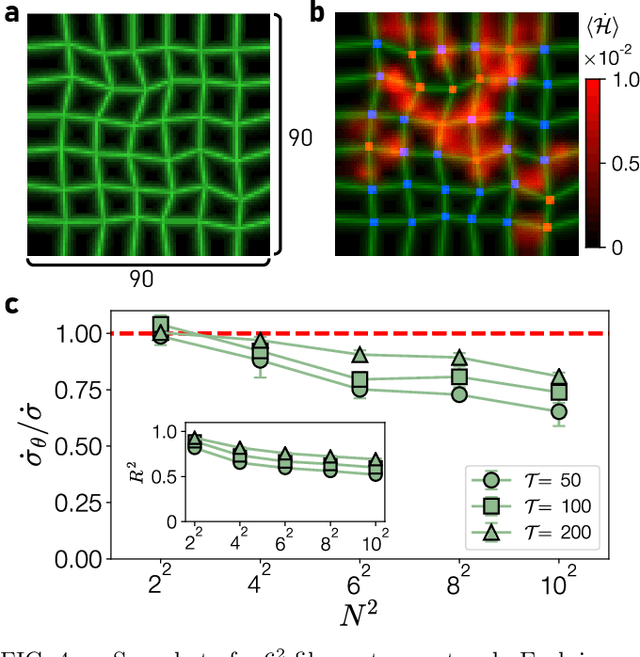
Quantifying entropy production (EP) is essential to understand stochastic systems at mesoscopic scales, such as living organisms or biological assemblies. However, without tracking the relevant variables, it is challenging to figure out where and to what extent EP occurs from recorded time-series image data from experiments. Here, applying a convolutional neural network (CNN), a powerful tool for image processing, we develop an estimation method for EP through an unsupervised learning algorithm that calculates only from movies. Together with an attention map of the CNN's last layer, our method can not only quantify stochastic EP but also produce the spatiotemporal pattern of the EP (dissipation map). We show that our method accurately measures the EP and creates a dissipation map in two nonequilibrium systems, the bead-spring model and a network of elastic filaments. We further confirm high performance even with noisy, low spatial resolution data, and partially observed situations. Our method will provide a practical way to obtain dissipation maps and ultimately contribute to uncovering the nonequilibrium nature of complex systems.

Learning entropy production via neural networks

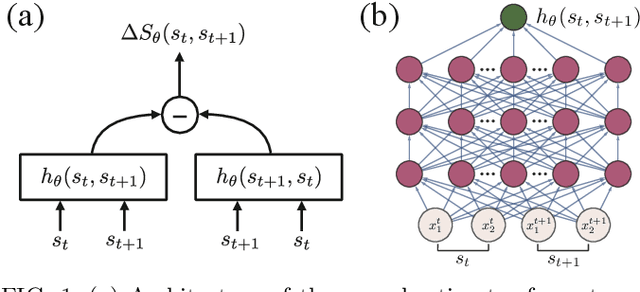
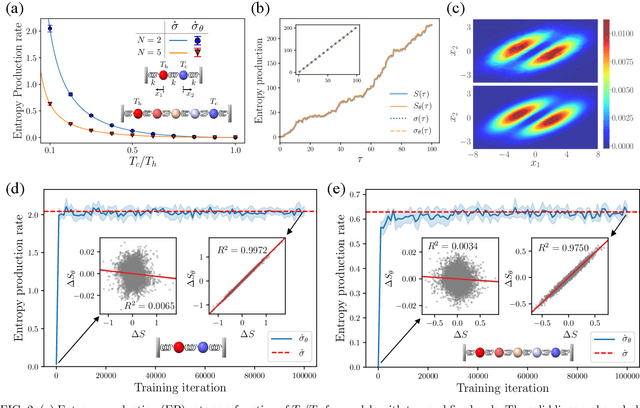
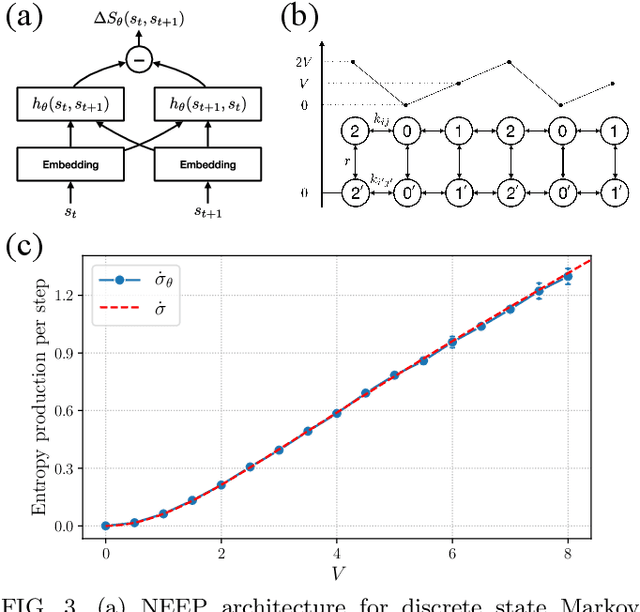
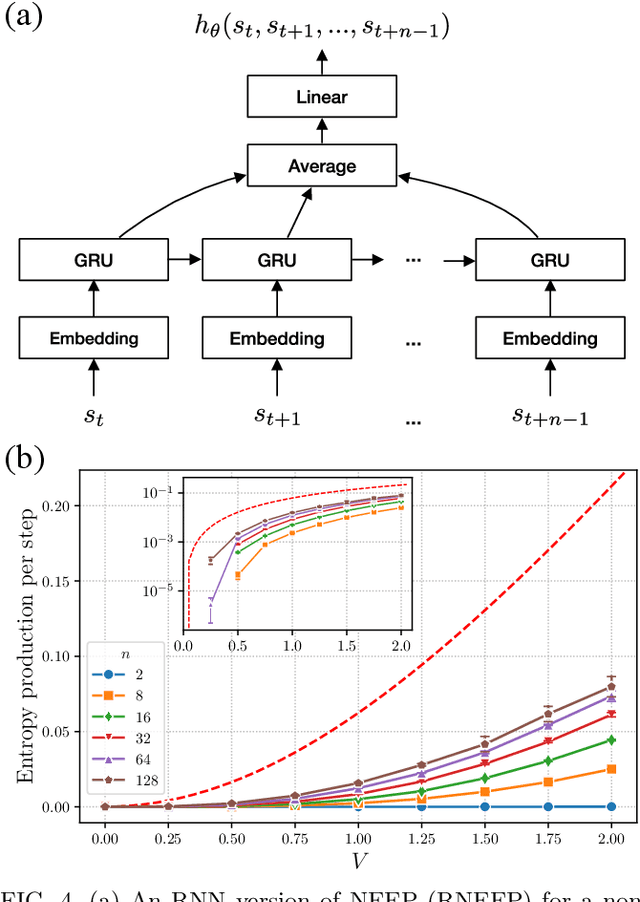
This Letter presents a neural estimator for entropy production, or NEEP, that estimates entropy production (EP) from trajectories without any prior knowledge of the system. For steady state, we rigorously prove that the estimator, which can be built up from different choices of deep neural networks, provides stochastic EP by optimizing the objective function proposed here. We verify the NEEP with the stochastic processes of the bead-spring and discrete flashing ratchet models, and also demonstrate that our method is applicable to high-dimensional data and non-Markovian systems.