Multi armed bandits and quantum channel oracles

Multi armed bandits are one of the theoretical pillars of reinforcement learning. Recently, the investigation of quantum algorithms for multi armed bandit problems was started, and it was found that a quadratic speed-up is possible when the arms and the randomness of the rewards of the arms can be queried in superposition. Here we introduce further bandit models where we only have limited access to the randomness of the rewards, but we can still query the arms in superposition. We show that this impedes any speed-up of quantum algorithms.

AutoML Two-Sample Test

Two-sample tests are important in statistics and machine learning, both as tools for scientific discovery as well as to detect distribution shifts. This led to the development of many sophisticated test procedures going beyond the standard supervised learning frameworks, whose usage can require specialized knowledge about two-sample testing. We use a simple test that takes the mean discrepancy of a witness function as the test statistic and prove that minimizing a squared loss leads to a witness with optimal testing power. This allows us to leverage recent advancements in AutoML. Without any user input about the problems at hand, and using the same method for all our experiments, our AutoML two-sample test achieves competitive performance on a diverse distribution shift benchmark as well as on challenging two-sample testing problems. We provide an implementation of the AutoML two-sample test in the Python package autotst.

Causal Inference Through the Structural Causal Marginal Problem

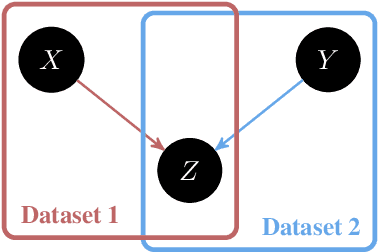
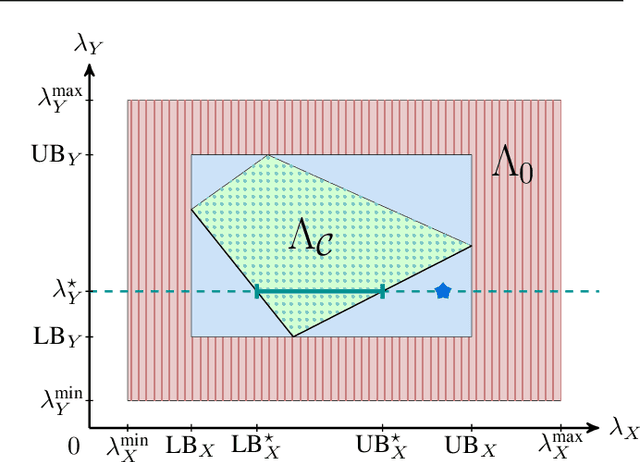
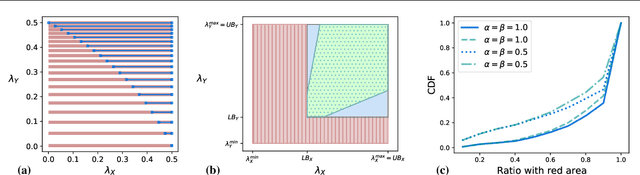
We introduce an approach to counterfactual inference based on merging information from multiple datasets. We consider a causal reformulation of the statistical marginal problem: given a collection of marginal structural causal models (SCMs) over distinct but overlapping sets of variables, determine the set of joint SCMs that are counterfactually consistent with the marginal ones. We formalise this approach for categorical SCMs using the response function formulation and show that it reduces the space of allowed marginal and joint SCMs. Our work thus highlights a new mode of falsifiability through additional variables, in contrast to the statistical one via additional data.

Quantum machine learning beyond kernel methods

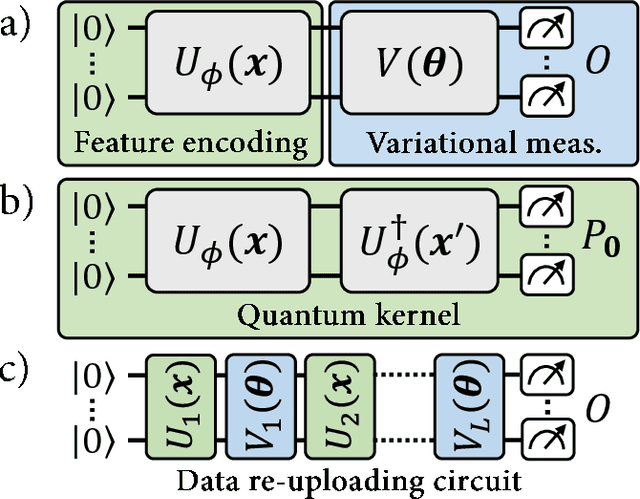
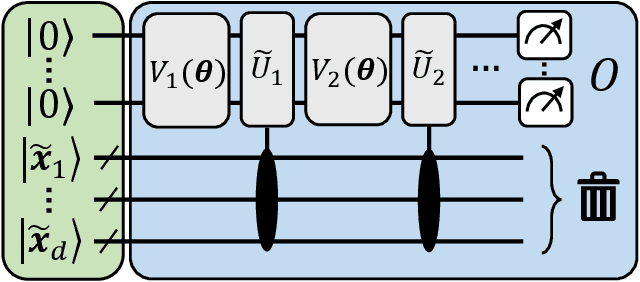
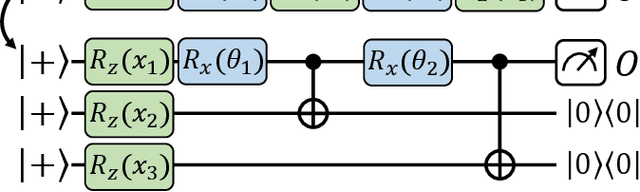
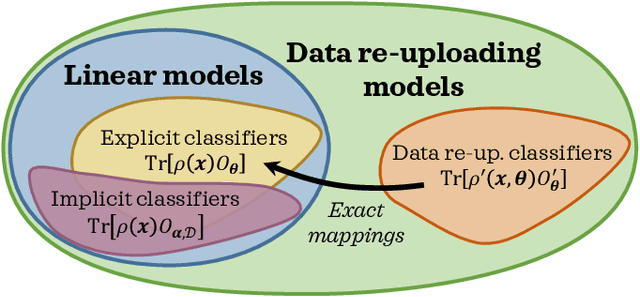
With noisy intermediate-scale quantum computers showing great promise for near-term applications, a number of machine learning algorithms based on parametrized quantum circuits have been suggested as possible means to achieve learning advantages. Yet, our understanding of how these quantum machine learning models compare, both to existing classical models and to each other, remains limited. A big step in this direction has been made by relating them to so-called kernel methods from classical machine learning. By building on this connection, previous works have shown that a systematic reformulation of many quantum machine learning models as kernel models was guaranteed to improve their training performance. In this work, we first extend the applicability of this result to a more general family of parametrized quantum circuit models called data re-uploading circuits. Secondly, we show, through simple constructions and numerical simulations, that models defined and trained variationally can exhibit a critically better generalization performance than their kernel formulations, which is the true figure of merit of machine learning tasks. Our results constitute another step towards a more comprehensive theory of quantum machine learning models next to kernel formulations.

The Inductive Bias of Quantum Kernels

It has been hypothesized that quantum computers may lend themselves well to applications in machine learning. In the present work, we analyze function classes defined via quantum kernels. Quantum computers offer the possibility to efficiently compute inner products of exponentially large density operators that are classically hard to compute. However, having an exponentially large feature space renders the problem of generalization hard. Furthermore, being able to evaluate inner products in high dimensional spaces efficiently by itself does not guarantee a quantum advantage, as already classically tractable kernels can correspond to high- or infinite-dimensional reproducing kernel Hilbert spaces (RKHS). We analyze the spectral properties of quantum kernels and find that we can expect an advantage if their RKHS is low dimensional and contains functions that are hard to compute classically. If the target function is known to lie in this class, this implies a quantum advantage, as the quantum computer can encode this inductive bias, whereas there is no classically efficient way to constrain the function class in the same way. However, we show that finding suitable quantum kernels is not easy because the kernel evaluation might require exponentially many measurements. In conclusion, our message is a somewhat sobering one: we conjecture that quantum machine learning models can offer speed-ups only if we manage to encode knowledge about the problem at hand into quantum circuits, while encoding the same bias into a classical model would be hard. These situations may plausibly occur when learning on data generated by a quantum process, however, they appear to be harder to come by for classical datasets.

An Optimal Witness Function for Two-Sample Testing

We propose data-dependent test statistics based on a one-dimensional witness function, which we call witness two-sample tests (WiTS tests). We first optimize the witness function by maximizing an asymptotic test-power objective and then use as the test statistic the difference in means of the witness evaluated on two held-out test samples. When the witness function belongs to a reproducing kernel Hilbert space, we show that the optimal witness is given via kernel Fisher discriminant analysis, whose solution we compute in closed form. We show that the WiTS test based on a characteristic kernel is consistent against any fixed alternative. Our experiments demonstrate that the WiTS test can achieve higher test power than existing two-sample tests with optimized kernels, suggesting that learning a high- or infinite-dimensional representation of the data may not be necessary for two-sample testing. The proposed procedure works beyond kernel methods, allowing practitioners to apply it within their preferred machine learning framework.

Learning Kernel Tests Without Data Splitting

Modern large-scale kernel-based tests such as maximum mean discrepancy (MMD) and kernelized Stein discrepancy (KSD) optimize kernel hyperparameters on a held-out sample via data splitting to obtain the most powerful test statistics. While data splitting results in a tractable null distribution, it suffers from a reduction in test power due to smaller test sample size. Inspired by the selective inference framework, we propose an approach that enables learning the hyperparameters and testing on the full sample without data splitting. Our approach can correctly calibrate the test in the presence of such dependency, and yield a test threshold in closed form. At the same significance level, our approach's test power is empirically larger than that of the data-splitting approach, regardless of its split proportion.

Quantum Mean Embedding of Probability Distributions

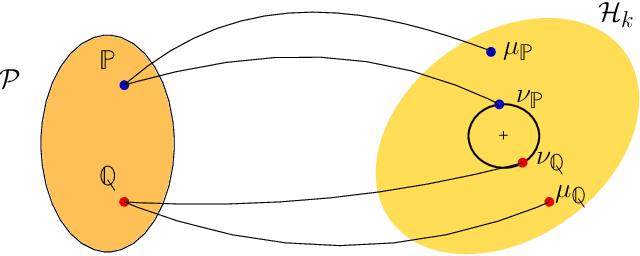
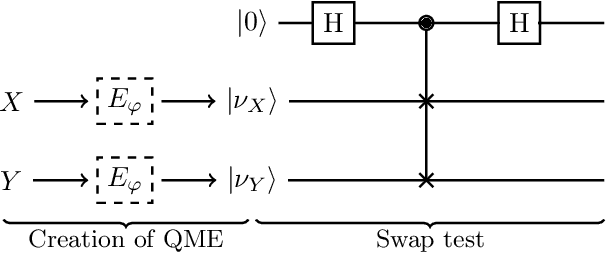
The kernel mean embedding of probability distributions is commonly used in machine learning as an injective mapping from distributions to functions in an infinite dimensional Hilbert space. It allows us, for example, to define a distance measure between probability distributions, called maximum mean discrepancy (MMD). In this work, we propose to represent probability distributions in a pure quantum state of a system that is described by an infinite dimensional Hilbert space. This enables us to work with an explicit representation of the mean embedding, whereas classically one can only work implicitly with an infinite dimensional Hilbert space through the use of the kernel trick. We show how this explicit representation can speed up methods that rely on inner products of mean embeddings and discuss the theoretical and experimental challenges that need to be solved in order to achieve these speedups.