Quantum Mean Embedding of Probability Distributions
Paper and Code
May 31, 2019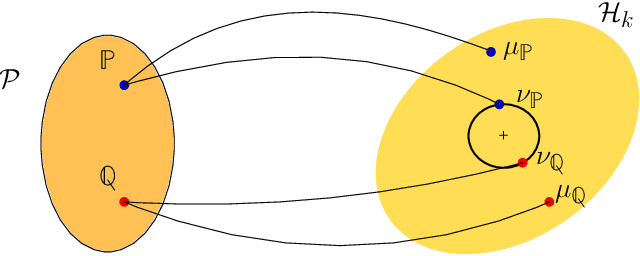
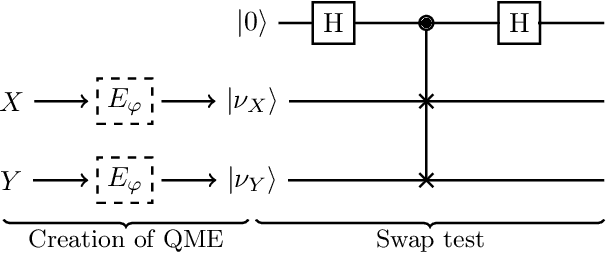
The kernel mean embedding of probability distributions is commonly used in machine learning as an injective mapping from distributions to functions in an infinite dimensional Hilbert space. It allows us, for example, to define a distance measure between probability distributions, called maximum mean discrepancy (MMD). In this work, we propose to represent probability distributions in a pure quantum state of a system that is described by an infinite dimensional Hilbert space. This enables us to work with an explicit representation of the mean embedding, whereas classically one can only work implicitly with an infinite dimensional Hilbert space through the use of the kernel trick. We show how this explicit representation can speed up methods that rely on inner products of mean embeddings and discuss the theoretical and experimental challenges that need to be solved in order to achieve these speedups.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge