Understanding polysemanticity in neural networks through coding theory

Despite substantial efforts, neural network interpretability remains an elusive goal, with previous research failing to provide succinct explanations of most single neurons' impact on the network output. This limitation is due to the polysemantic nature of most neurons, whereby a given neuron is involved in multiple unrelated network states, complicating the interpretation of that neuron. In this paper, we apply tools developed in neuroscience and information theory to propose both a novel practical approach to network interpretability and theoretical insights into polysemanticity and the density of codes. We infer levels of redundancy in the network's code by inspecting the eigenspectrum of the activation's covariance matrix. Furthermore, we show how random projections can reveal whether a network exhibits a smooth or non-differentiable code and hence how interpretable the code is. This same framework explains the advantages of polysemantic neurons to learning performance and explains trends found in recent results by Elhage et al.~(2022). Our approach advances the pursuit of interpretability in neural networks, providing insights into their underlying structure and suggesting new avenues for circuit-level interpretability.

Shadows of quantum machine learning

Quantum machine learning is often highlighted as one of the most promising uses for a quantum computer to solve practical problems. However, a major obstacle to the widespread use of quantum machine learning models in practice is that these models, even once trained, still require access to a quantum computer in order to be evaluated on new data. To solve this issue, we suggest that following the training phase of a quantum model, a quantum computer could be used to generate what we call a classical shadow of this model, i.e., a classically computable approximation of the learned function. While recent works already explore this idea and suggest approaches to construct such shadow models, they also raise the possibility that a completely classical model could be trained instead, thus circumventing the need for a quantum computer in the first place. In this work, we take a novel approach to define shadow models based on the frameworks of quantum linear models and classical shadow tomography. This approach allows us to show that there exist shadow models which can solve certain learning tasks that are intractable for fully classical models, based on widely-believed cryptography assumptions. We also discuss the (un)likeliness that all quantum models could be shadowfiable, based on common assumptions in complexity theory.

High Dimensional Quantum Learning With Small Quantum Computers

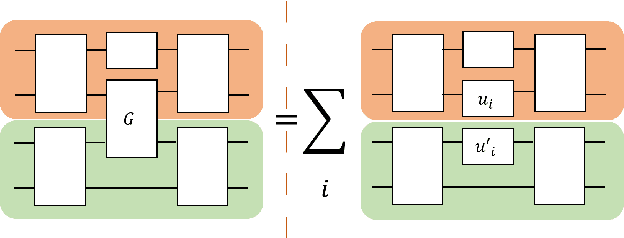
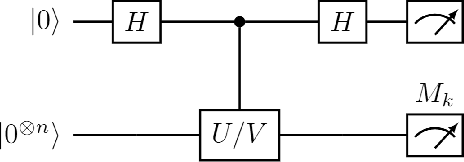
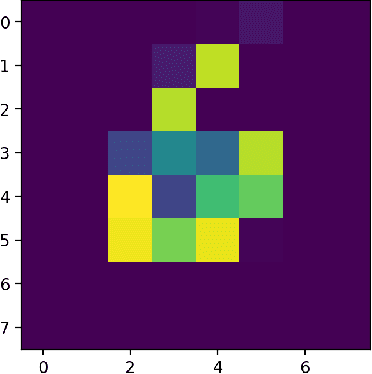
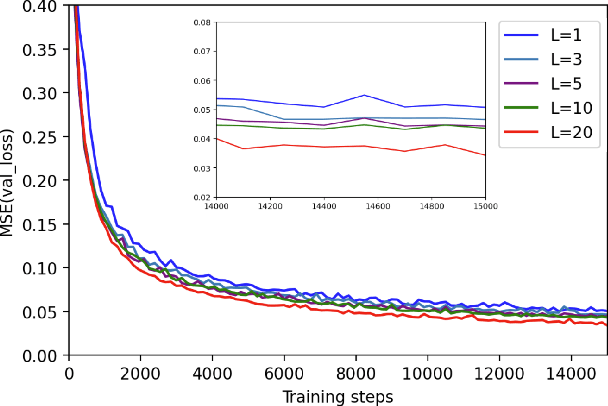
Quantum computers hold great promise to enhance machine learning, but their current qubit counts restrict the realisation of this promise. In an attempt to placate this limitation techniques can be applied for evaluating a quantum circuit using a machine with fewer qubits than the circuit naively requires. These techniques work by evaluating many smaller circuits on the smaller machine, that are then combined in a polynomial to replicate the output of the larger machine. This scheme requires more circuit evaluations than are practical for general circuits. However, we investigate the possibility that for certain applications many of these subcircuits are superfluous, and that a much smaller sum is sufficient to estimate the full circuit. We construct a machine learning model that may be capable of approximating the outputs of the larger circuit with much fewer circuit evaluations. We successfully apply our model to the task of digit recognition, using simulated quantum computers much smaller than the data dimension. The model is also applied to the task of approximating a random 10 qubit PQC with simulated access to a 5 qubit computer, even with only relatively modest number of circuits our model provides an accurate approximation of the 10 qubit PQCs output, superior to a neural network attempt. The developed method might be useful for implementing quantum models on larger data throughout the NISQ era.