Artificially intelligent Maxwell's demon for optimal control of open quantum systems

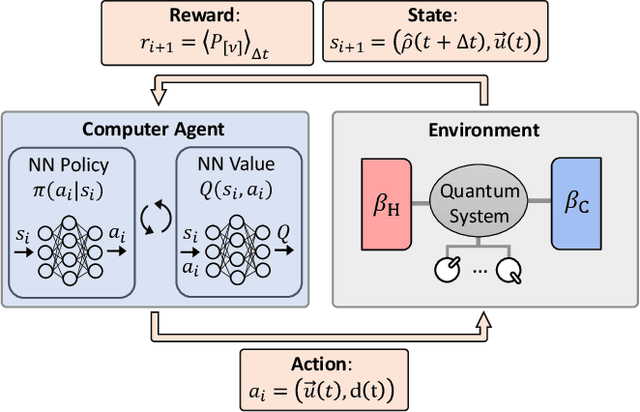
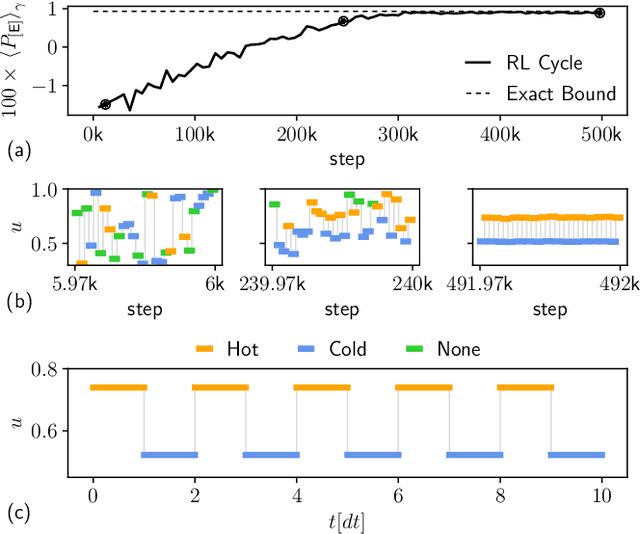
Feedback control of open quantum systems is of fundamental importance for practical applications in various contexts, ranging from quantum computation to quantum error correction and quantum metrology. Its use in the context of thermodynamics further enables the study of the interplay between information and energy. However, deriving optimal feedback control strategies is highly challenging, as it involves the optimal control of open quantum systems, the stochastic nature of quantum measurement, and the inclusion of policies that maximize a long-term time- and trajectory-averaged goal. In this work, we employ a reinforcement learning approach to automate and capture the role of a quantum Maxwell's demon: the agent takes the literal role of discovering optimal feedback control strategies in qubit-based systems that maximize a trade-off between measurement-powered cooling and measurement efficiency. Considering weak or projective quantum measurements, we explore different regimes based on the ordering between the thermalization, the measurement, and the unitary feedback timescales, finding different and highly non-intuitive, yet interpretable, strategies. In the thermalization-dominated regime, we find strategies with elaborate finite-time thermalization protocols conditioned on measurement outcomes. In the measurement-dominated regime, we find that optimal strategies involve adaptively measuring different qubit observables reflecting the acquired information, and repeating multiple weak measurements until the quantum state is "sufficiently pure", leading to random walks in state space. Finally, we study the case when all timescales are comparable, finding new feedback control strategies that considerably outperform more intuitive ones. We discuss a two-qubit example where we explore the role of entanglement and conclude discussing the scaling of our results to quantum many-body systems.

Driving black-box quantum thermal machines with optimal power/efficiency trade-offs using reinforcement learning

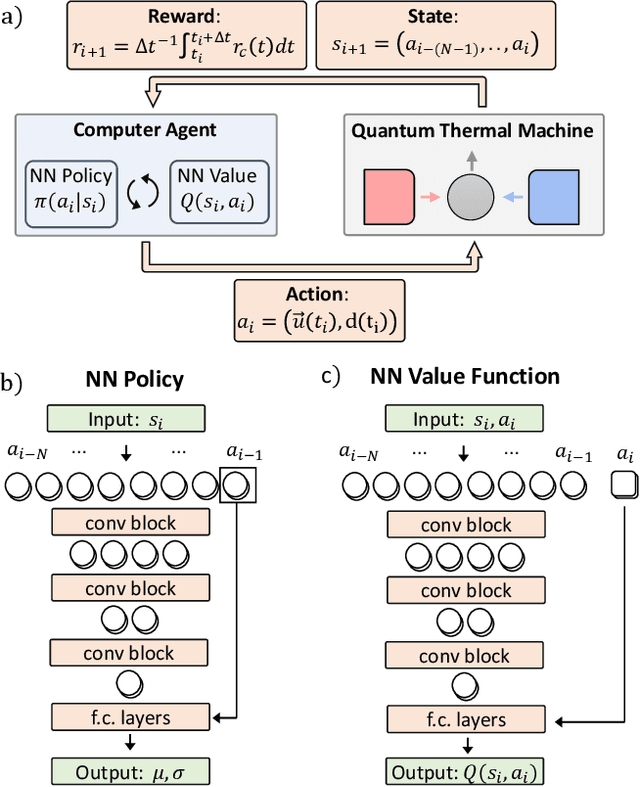
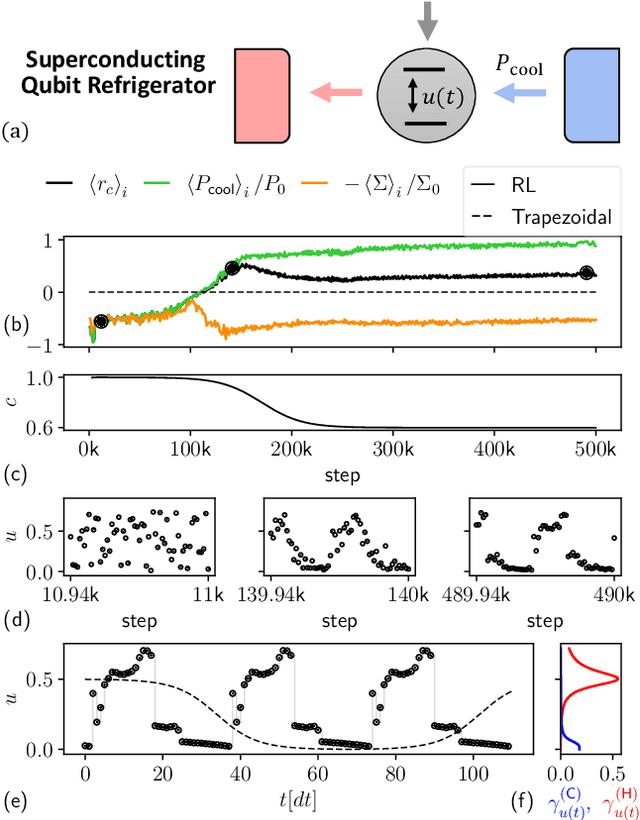
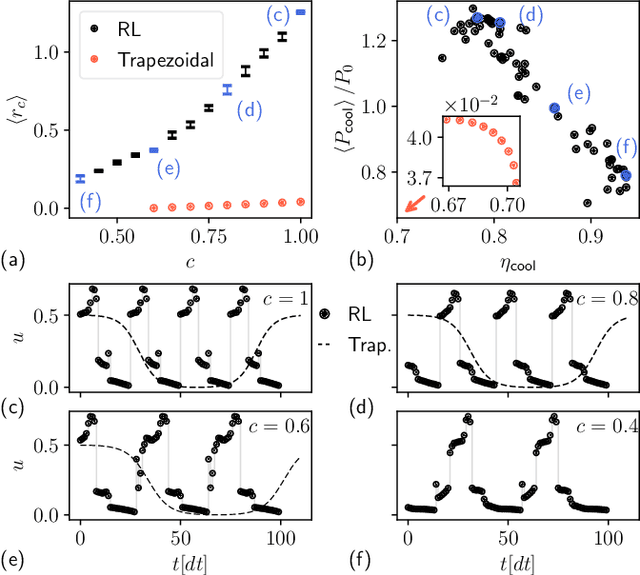
The optimal control of non-equilibrium open quantum systems is a challenging task but has a key role in improving existing quantum information processing technologies. We introduce a general model-free framework based on Reinforcement Learning to identify out-of-equilibrium thermodynamic cycles that are Pareto optimal trade-offs between power and efficiency for quantum heat engines and refrigerators. The method does not require any knowledge of the quantum thermal machine, nor of the system model, nor of the quantum state. Instead, it only observes the heat fluxes, so it is both applicable to simulations and experimental devices. We test our method identifying Pareto-optimal trade-offs between power and efficiency in two systems: an experimentally realistic refrigerator based on a superconducting qubit, where we identify non-intuitive control sequences that reduce quantum friction and outperform previous cycles proposed in literature; and a heat engine based on a quantum harmonic oscillator, where we find cycles with an elaborate structure that outperform the optimized Otto cycle.

Identifying optimal cycles in quantum thermal machines with reinforcement-learning

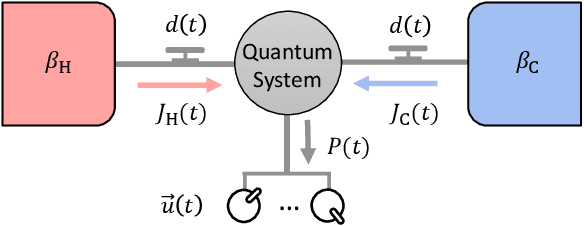
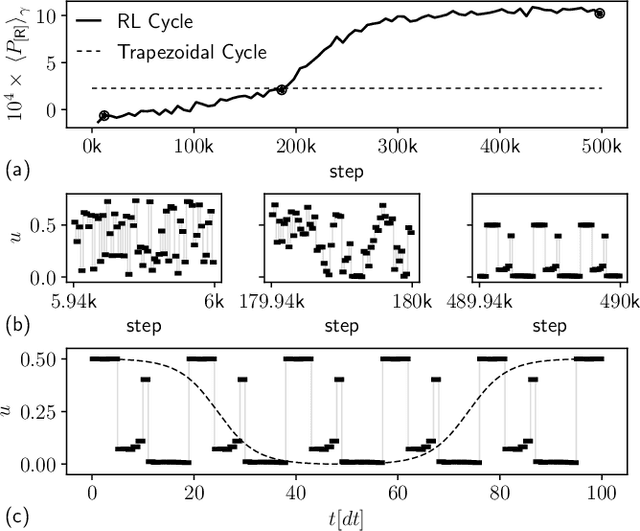
The optimal control of open quantum systems is a challenging task but has a key role in improving existing quantum information processing technologies. We introduce a general framework based on Reinforcement Learning to discover optimal thermodynamic cycles that maximize the power of out-of-equilibrium quantum heat engines and refrigerators. We apply our method, based on the soft actor-critic algorithm, to three systems: a benchmark two-level system heat engine, where we find the optimal known cycle; an experimentally realistic refrigerator based on a superconducting qubit that generates coherence, where we find a non-intuitive control sequence that outperform previous cycles proposed in literature; a heat engine based on a quantum harmonic oscillator, where we find a cycle with an elaborate structure that outperforms the optimized Otto cycle. We then evaluate the corresponding efficiency at maximum power.