Artificially intelligent Maxwell's demon for optimal control of open quantum systems

Feedback control of open quantum systems is of fundamental importance for practical applications in various contexts, ranging from quantum computation to quantum error correction and quantum metrology. Its use in the context of thermodynamics further enables the study of the interplay between information and energy. However, deriving optimal feedback control strategies is highly challenging, as it involves the optimal control of open quantum systems, the stochastic nature of quantum measurement, and the inclusion of policies that maximize a long-term time- and trajectory-averaged goal. In this work, we employ a reinforcement learning approach to automate and capture the role of a quantum Maxwell's demon: the agent takes the literal role of discovering optimal feedback control strategies in qubit-based systems that maximize a trade-off between measurement-powered cooling and measurement efficiency. Considering weak or projective quantum measurements, we explore different regimes based on the ordering between the thermalization, the measurement, and the unitary feedback timescales, finding different and highly non-intuitive, yet interpretable, strategies. In the thermalization-dominated regime, we find strategies with elaborate finite-time thermalization protocols conditioned on measurement outcomes. In the measurement-dominated regime, we find that optimal strategies involve adaptively measuring different qubit observables reflecting the acquired information, and repeating multiple weak measurements until the quantum state is "sufficiently pure", leading to random walks in state space. Finally, we study the case when all timescales are comparable, finding new feedback control strategies that considerably outperform more intuitive ones. We discuss a two-qubit example where we explore the role of entanglement and conclude discussing the scaling of our results to quantum many-body systems.

The Best Radar Ranging Pulse to Resolve Two Reflectors

Previous work established fundamental bounds on subwavelength resolution for the radar range resolution problem, called superradar [Phys. Rev. Appl. 20, 064046 (2023)]. In this work, we identify the optimal waveforms for distinguishing the range resolution between two reflectors of identical strength. We discuss both the unnormalized optimal waveform as well as the best square-integrable pulse, and their variants. Using orthogonal function theory, we give an explicit algorithm to optimize the wave pulse in finite time to have the best performance. We also explore range resolution estimation with unnormalized waveforms with multi-parameter methods to also independently estimate loss and time of arrival. These results are consistent with the earlier single parameter approach of range resolution only and give deeper insight into the ranging estimation problem. Experimental results are presented using radio pulse reflections inside coaxial cables, showing robust range resolution smaller than a tenth of the inverse bandedge, with uncertainties close to the derived Cram\'er-Rao bound.

Confocal super-resolution microscopy based on a spatial mode sorter

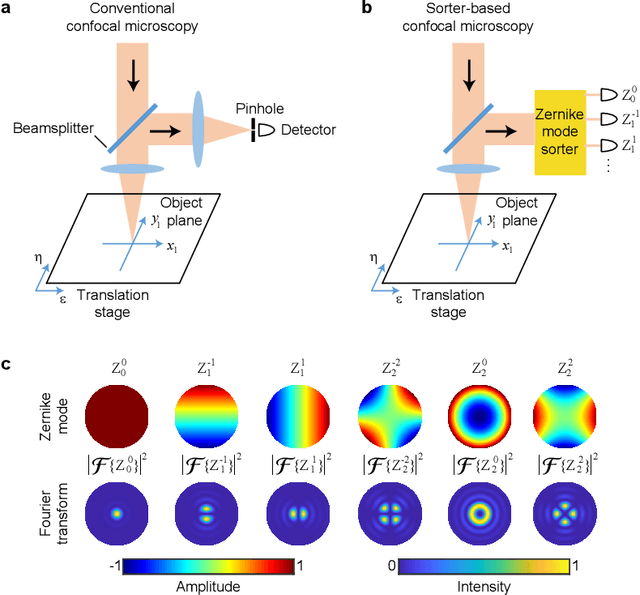
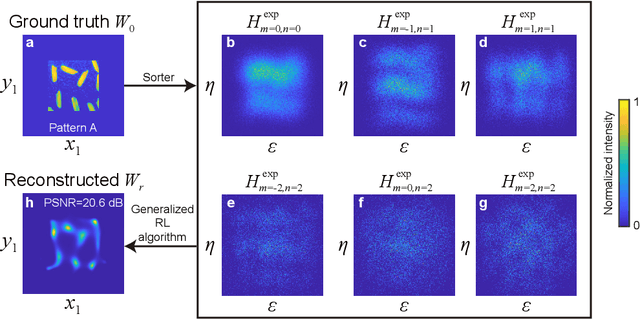
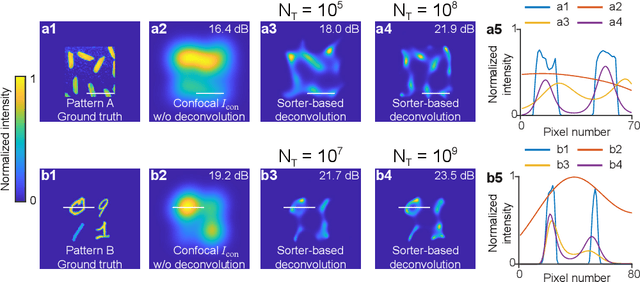
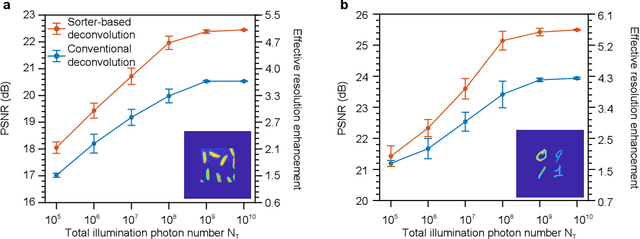
Spatial resolution is one of the most important specifications of an imaging system. Recent results in quantum parameter estimation theory reveal that an arbitrarily small distance between two incoherent point sources can always be efficiently determined through the use of a spatial mode sorter. However, extending this procedure to a general object consisting of many incoherent point sources remains challenging, due to the intrinsic complexity of multi-parameter estimation problems. Here, we generalize the Richardson-Lucy (RL) deconvolution algorithm to address this challenge. We simulate its application to an incoherent confocal microscope, with a Zernike spatial mode sorter replacing the pinhole used in a conventional confocal microscope. We test different spatially incoherent objects of arbitrary geometry, and we find that sorter-based microscopy can achieve more than 5-fold resolution enhancement over a diffraction-limited image. In addition, the resolution enhancement of sorter-based microscopy is on average over 30% higher than that of a conventional confocal microscope using the standard RL deconvolution algorithm. Our method could potentially be used in diverse applications such as fluorescent microscopy and astronomical imaging.