Confocal super-resolution microscopy based on a spatial mode sorter
Paper and Code
Jan 11, 2021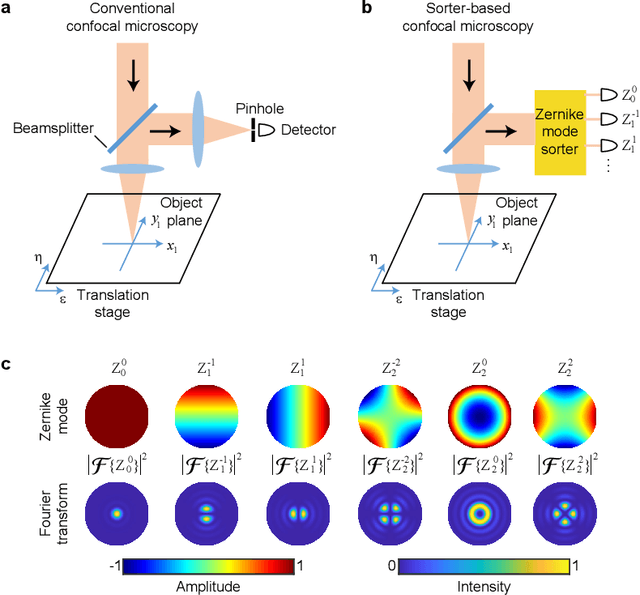
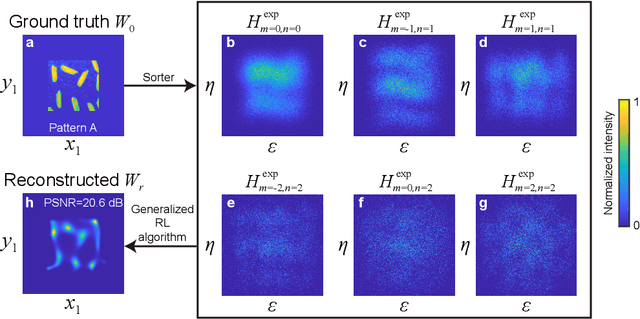
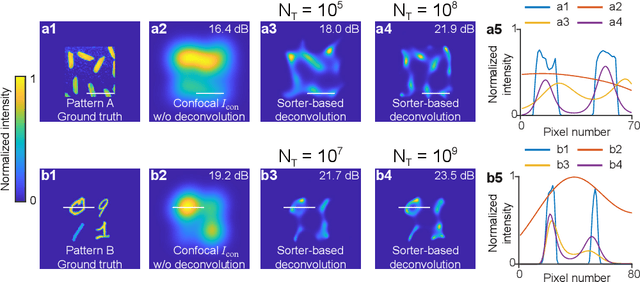
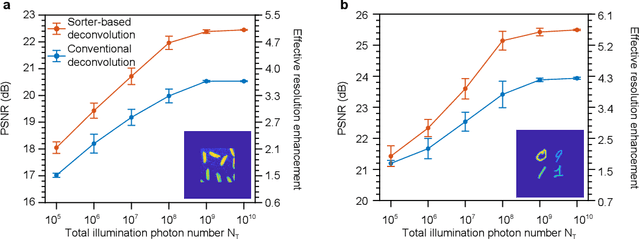
Spatial resolution is one of the most important specifications of an imaging system. Recent results in quantum parameter estimation theory reveal that an arbitrarily small distance between two incoherent point sources can always be efficiently determined through the use of a spatial mode sorter. However, extending this procedure to a general object consisting of many incoherent point sources remains challenging, due to the intrinsic complexity of multi-parameter estimation problems. Here, we generalize the Richardson-Lucy (RL) deconvolution algorithm to address this challenge. We simulate its application to an incoherent confocal microscope, with a Zernike spatial mode sorter replacing the pinhole used in a conventional confocal microscope. We test different spatially incoherent objects of arbitrary geometry, and we find that sorter-based microscopy can achieve more than 5-fold resolution enhancement over a diffraction-limited image. In addition, the resolution enhancement of sorter-based microscopy is on average over 30% higher than that of a conventional confocal microscope using the standard RL deconvolution algorithm. Our method could potentially be used in diverse applications such as fluorescent microscopy and astronomical imaging.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge