The Best Radar Ranging Pulse to Resolve Two Reflectors

Previous work established fundamental bounds on subwavelength resolution for the radar range resolution problem, called superradar [Phys. Rev. Appl. 20, 064046 (2023)]. In this work, we identify the optimal waveforms for distinguishing the range resolution between two reflectors of identical strength. We discuss both the unnormalized optimal waveform as well as the best square-integrable pulse, and their variants. Using orthogonal function theory, we give an explicit algorithm to optimize the wave pulse in finite time to have the best performance. We also explore range resolution estimation with unnormalized waveforms with multi-parameter methods to also independently estimate loss and time of arrival. These results are consistent with the earlier single parameter approach of range resolution only and give deeper insight into the ranging estimation problem. Experimental results are presented using radio pulse reflections inside coaxial cables, showing robust range resolution smaller than a tenth of the inverse bandedge, with uncertainties close to the derived Cram\'er-Rao bound.

Learning to Utilize Correlated Auxiliary Classical or Quantum Noise

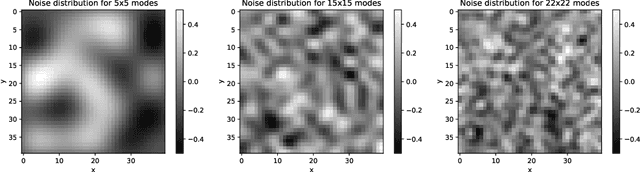
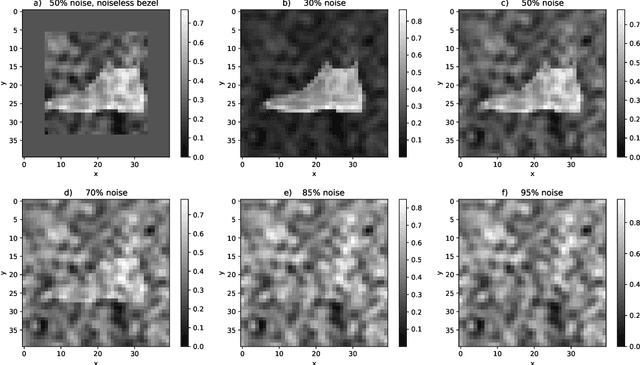
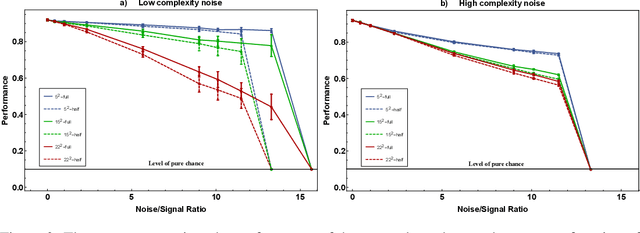
This paper has two messages. First, we demonstrate that neural networks can learn to exploit correlations between noisy data and suitable auxiliary noise. In effect, the network learns to use the correlated auxiliary noise as an approximate key to decipher its noisy input data. Second, we show that the scaling behavior with increasing noise is such that future quantum machines should possess an advantage. For a concrete example, we reduce the image classification performance of convolutional neural networks (CNNs) by adding noise of different amounts and quality to the input images. We then demonstrate that the CNNs are able to partly recover their performance if, along with each noisy image, they are given auxiliary noise that is correlated with the image noise. We analyze the scaling of a CNN ability to learn and utilize these noise correlations as the level, dimensionality, or complexity of the noise is increased. We thereby find numerical and theoretical indications that quantum machines, due to their efficiency in representing complex correlations, could possess a significant advantage over classical machines.