Digital-analog quantum learning on Rydberg atom arrays

We propose hybrid digital-analog learning algorithms on Rydberg atom arrays, combining the potentially practical utility and near-term realizability of quantum learning with the rapidly scaling architectures of neutral atoms. Our construction requires only single-qubit operations in the digital setting and global driving according to the Rydberg Hamiltonian in the analog setting. We perform a comprehensive numerical study of our algorithm on both classical and quantum data, given respectively by handwritten digit classification and unsupervised quantum phase boundary learning. We show in the two representative problems that digital-analog learning is not only feasible in the near term, but also requires shorter circuit depths and is more robust to realistic error models as compared to digital learning schemes. Our results suggest that digital-analog learning opens a promising path towards improved variational quantum learning experiments in the near term.

Learning quantum symmetries with interactive quantum-classical variational algorithms

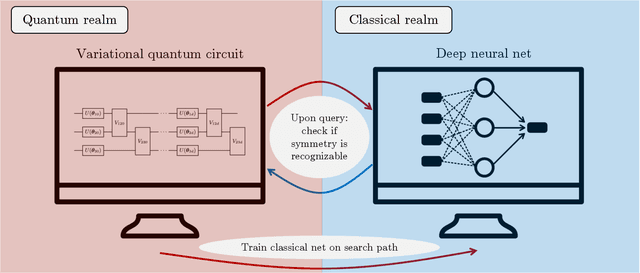
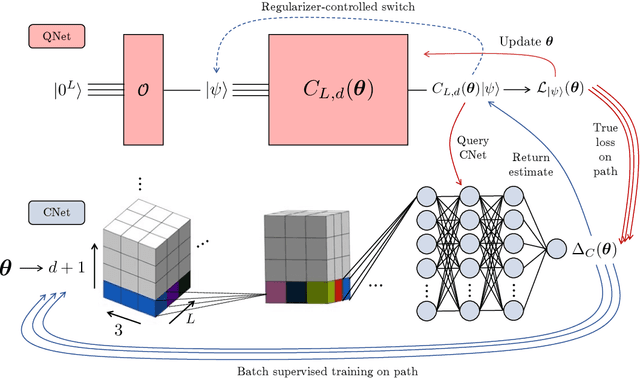
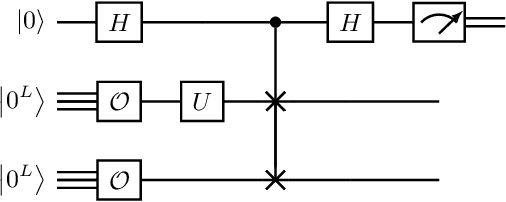
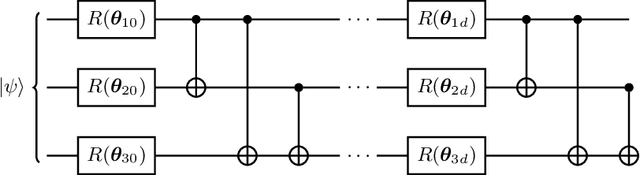
A symmetry of a state $\lvert \psi \rangle$ is a unitary operator of which $\lvert \psi \rangle$ is an eigenvector. When $\lvert \psi \rangle$ is an unknown state supplied by a black-box oracle, the state's symmetries serve to characterize it, and often relegate much of the desired information about $\lvert \psi \rangle$. In this paper, we develop a variational hybrid quantum-classical learning scheme to systematically probe for symmetries of $\lvert \psi \rangle$ with no a priori assumptions about the state. This procedure can be used to learn various symmetries at the same time. In order to avoid re-learning already known symmetries, we introduce an interactive protocol with a classical deep neural net. The classical net thereby regularizes against repetitive findings and allows our algorithm to terminate empirically with all possible symmetries found. Our scheme can be implemented efficiently on average with non-local SWAP gates; we also give a less efficient algorithm with only local operations, which may be more appropriate for current noisy quantum devices. We demonstrate our algorithm on representative families of states.