Non-native Quantum Generative Optimization with Adversarial Autoencoders

Large-scale optimization problems are prevalent in several fields, including engineering, finance, and logistics. However, most optimization problems cannot be efficiently encoded onto a physical system because the existing quantum samplers have too few qubits. Another typical limiting factor is that the optimization constraints are not compatible with the native cost Hamiltonian. This work presents a new approach to address these challenges. We introduce the adversarial quantum autoencoder model (AQAM) that can be used to map large-scale optimization problems onto existing quantum samplers while simultaneously optimizing the problem through latent quantum-enhanced Boltzmann sampling. We demonstrate the AQAM on a neutral atom sampler, and showcase the model by optimizing 64px by 64px unit cells that represent a broad-angle filter metasurface applicable to improving the coherence of neutral atom devices. Using 12-atom simulations, we demonstrate that the AQAM achieves a lower Renyi divergence and a larger spectral gap when compared to classical Markov Chain Monte Carlo samplers. Our work paves the way to more efficient mapping of conventional optimization problems into existing quantum samplers.

Digital-analog quantum learning on Rydberg atom arrays

We propose hybrid digital-analog learning algorithms on Rydberg atom arrays, combining the potentially practical utility and near-term realizability of quantum learning with the rapidly scaling architectures of neutral atoms. Our construction requires only single-qubit operations in the digital setting and global driving according to the Rydberg Hamiltonian in the analog setting. We perform a comprehensive numerical study of our algorithm on both classical and quantum data, given respectively by handwritten digit classification and unsupervised quantum phase boundary learning. We show in the two representative problems that digital-analog learning is not only feasible in the near term, but also requires shorter circuit depths and is more robust to realistic error models as compared to digital learning schemes. Our results suggest that digital-analog learning opens a promising path towards improved variational quantum learning experiments in the near term.

Enhancing Generative Models via Quantum Correlations

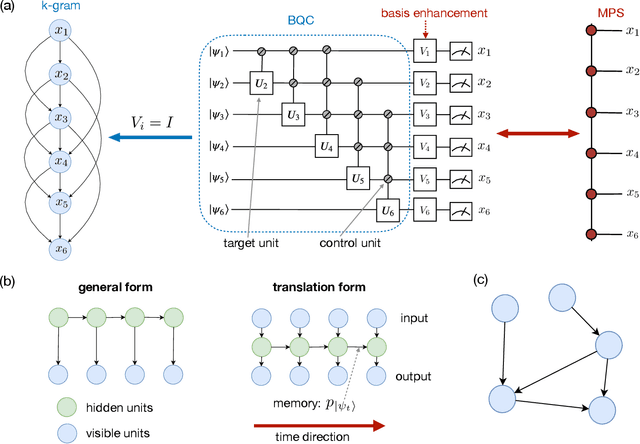
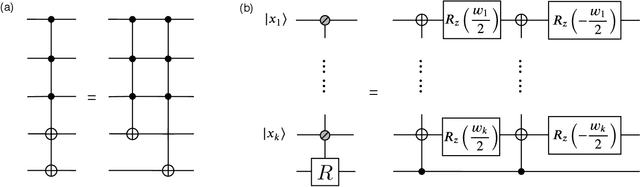
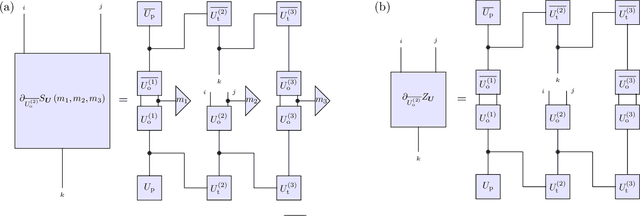
Generative modeling using samples drawn from the probability distribution constitutes a powerful approach for unsupervised machine learning. Quantum mechanical systems can produce probability distributions that exhibit quantum correlations which are difficult to capture using classical models. We show theoretically that such quantum correlations provide a powerful resource for generative modeling. In particular, we provide an unconditional proof of separation in expressive power between a class of widely-used generative models, known as Bayesian networks, and its minimal quantum extension. We show that this expressivity advantage is associated with quantum nonlocality and quantum contextuality. Furthermore, we numerically test this separation on standard machine learning data sets and show that it holds for practical problems. The possibility of quantum advantage demonstrated in this work not only sheds light on the design of useful quantum machine learning protocols but also provides inspiration to draw on ideas from quantum foundations to improve purely classical algorithms.