Enhancing Quantum Memory Lifetime with Measurement-Free Local Error Correction and Reinforcement Learning

Reliable quantum computation requires systematic identification and correction of errors that occur and accumulate in quantum hardware. To diagnose and correct such errors, standard quantum error-correcting protocols utilize $\textit{global}$ error information across the system obtained by mid-circuit readout of ancillary qubits. We investigate circuit-level error-correcting protocols that are measurement-free and based on $\textit{local}$ error information. Such a local error correction (LEC) circuit consists of faulty multi-qubit gates to perform both syndrome extraction and ancilla-controlled error removal. We develop and implement a reinforcement learning framework that takes a fixed set of faulty gates as inputs and outputs an optimized LEC circuit. To evaluate this approach, we quantitatively characterize an extension of logical qubit lifetime by a noisy LEC circuit. For the 2D classical Ising model and 4D toric code, our optimized LEC circuit performs better at extending a memory lifetime compared to a conventional LEC circuit based on Toom's rule in a sub-threshold gate error regime. We further show that such circuits can be used to reduce the rate of mid-circuit readouts to preserve a 2D toric code memory. Finally, we discuss the application of the LEC protocol on dissipative preparation of quantum states with topological phases.

Hardware-efficient learning of quantum many-body states

Efficient characterization of highly entangled multi-particle systems is an outstanding challenge in quantum science. Recent developments have shown that a modest number of randomized measurements suffices to learn many properties of a quantum many-body system. However, implementing such measurements requires complete control over individual particles, which is unavailable in many experimental platforms. In this work, we present rigorous and efficient algorithms for learning quantum many-body states in systems with any degree of control over individual particles, including when every particle is subject to the same global field and no additional ancilla particles are available. We numerically demonstrate the effectiveness of our algorithms for estimating energy densities in a U(1) lattice gauge theory and classifying topological order using very limited measurement capabilities.

Machine learning discovery of new phases in programmable quantum simulator snapshots

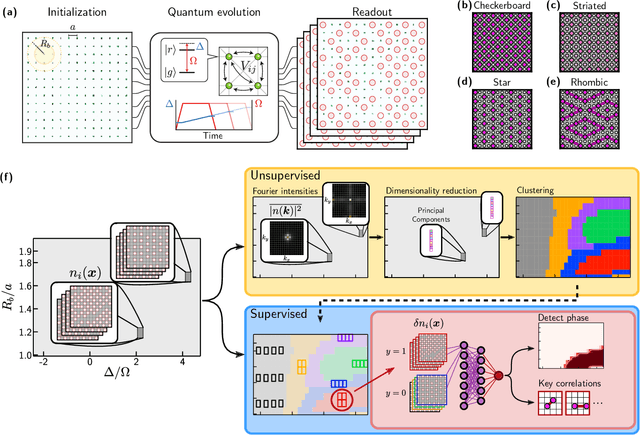
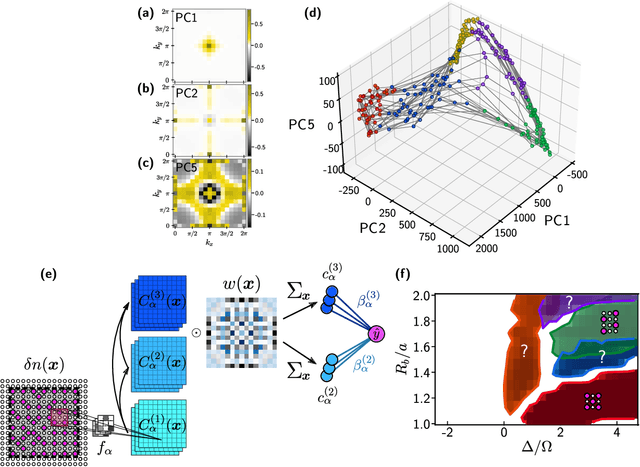
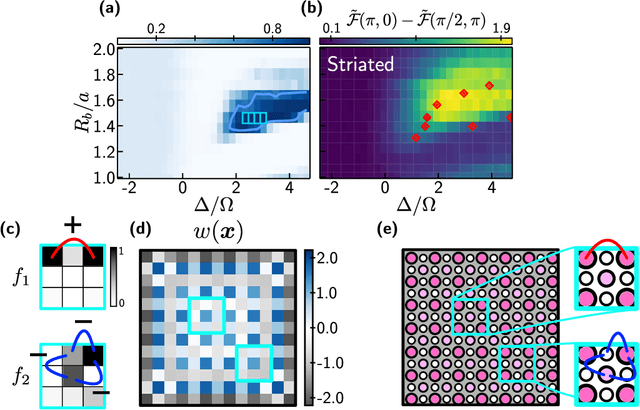
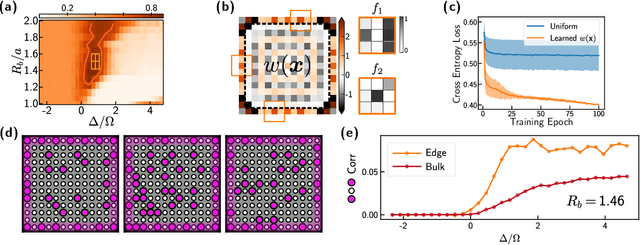
Machine learning has recently emerged as a promising approach for studying complex phenomena characterized by rich datasets. In particular, data-centric approaches lend to the possibility of automatically discovering structures in experimental datasets that manual inspection may miss. Here, we introduce an interpretable unsupervised-supervised hybrid machine learning approach, the hybrid-correlation convolutional neural network (Hybrid-CCNN), and apply it to experimental data generated using a programmable quantum simulator based on Rydberg atom arrays. Specifically, we apply Hybrid-CCNN to analyze new quantum phases on square lattices with programmable interactions. The initial unsupervised dimensionality reduction and clustering stage first reveals five distinct quantum phase regions. In a second supervised stage, we refine these phase boundaries and characterize each phase by training fully interpretable CCNNs and extracting the relevant correlations for each phase. The characteristic spatial weightings and snippets of correlations specifically recognized in each phase capture quantum fluctuations in the striated phase and identify two previously undetected phases, the rhombic and boundary-ordered phases. These observations demonstrate that a combination of programmable quantum simulators with machine learning can be used as a powerful tool for detailed exploration of correlated quantum states of matter.

Enhancing Generative Models via Quantum Correlations

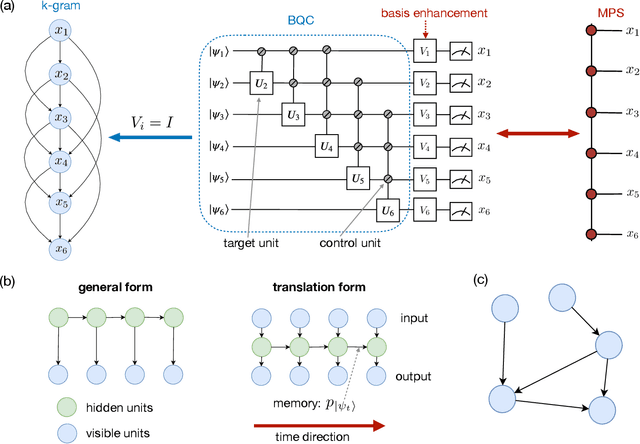
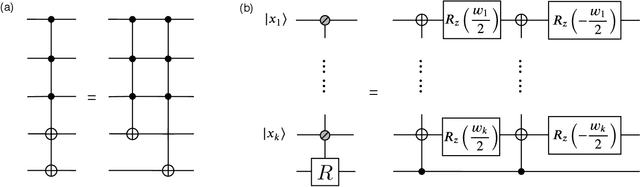
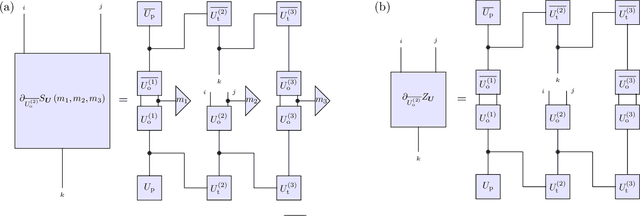
Generative modeling using samples drawn from the probability distribution constitutes a powerful approach for unsupervised machine learning. Quantum mechanical systems can produce probability distributions that exhibit quantum correlations which are difficult to capture using classical models. We show theoretically that such quantum correlations provide a powerful resource for generative modeling. In particular, we provide an unconditional proof of separation in expressive power between a class of widely-used generative models, known as Bayesian networks, and its minimal quantum extension. We show that this expressivity advantage is associated with quantum nonlocality and quantum contextuality. Furthermore, we numerically test this separation on standard machine learning data sets and show that it holds for practical problems. The possibility of quantum advantage demonstrated in this work not only sheds light on the design of useful quantum machine learning protocols but also provides inspiration to draw on ideas from quantum foundations to improve purely classical algorithms.