MQFL-FHE: Multimodal Quantum Federated Learning Framework with Fully Homomorphic Encryption

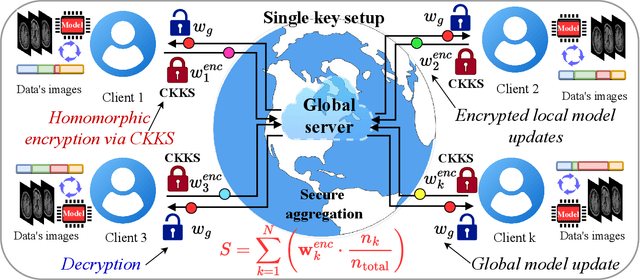
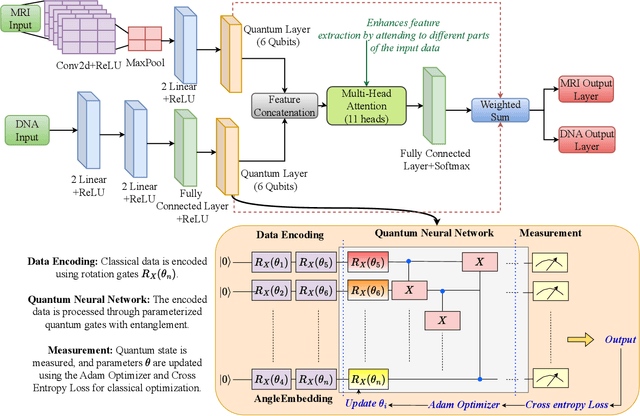
The integration of fully homomorphic encryption (FHE) in federated learning (FL) has led to significant advances in data privacy. However, during the aggregation phase, it often results in performance degradation of the aggregated model, hindering the development of robust representational generalization. In this work, we propose a novel multimodal quantum federated learning framework that utilizes quantum computing to counteract the performance drop resulting from FHE. For the first time in FL, our framework combines a multimodal quantum mixture of experts (MQMoE) model with FHE, incorporating multimodal datasets for enriched representation and task-specific learning. Our MQMoE framework enhances performance on multimodal datasets and combined genomics and brain MRI scans, especially for underrepresented categories. Our results also demonstrate that the quantum-enhanced approach mitigates the performance degradation associated with FHE and improves classification accuracy across diverse datasets, validating the potential of quantum interventions in enhancing privacy in FL.

Federated Learning in Chemical Engineering: A Tutorial on a Framework for Privacy-Preserving Collaboration Across Distributed Data Sources

Federated Learning (FL) is a decentralized machine learning approach that has gained attention for its potential to enable collaborative model training across clients while protecting data privacy, making it an attractive solution for the chemical industry. This work aims to provide the chemical engineering community with an accessible introduction to the discipline. Supported by a hands-on tutorial and a comprehensive collection of examples, it explores the application of FL in tasks such as manufacturing optimization, multimodal data integration, and drug discovery while addressing the unique challenges of protecting proprietary information and managing distributed datasets. The tutorial was built using key frameworks such as $\texttt{Flower}$ and $\texttt{TensorFlow Federated}$ and was designed to provide chemical engineers with the right tools to adopt FL in their specific needs. We compare the performance of FL against centralized learning across three different datasets relevant to chemical engineering applications, demonstrating that FL will often maintain or improve classification performance, particularly for complex and heterogeneous data. We conclude with an outlook on the open challenges in federated learning to be tackled and current approaches designed to remediate and improve this framework.

Federated Learning with Quantum Computing and Fully Homomorphic Encryption: A Novel Computing Paradigm Shift in Privacy-Preserving ML

The widespread deployment of products powered by machine learning models is raising concerns around data privacy and information security worldwide. To address this issue, Federated Learning was first proposed as a privacy-preserving alternative to conventional methods that allow multiple learning clients to share model knowledge without disclosing private data. A complementary approach known as Fully Homomorphic Encryption (FHE) is a quantum-safe cryptographic system that enables operations to be performed on encrypted weights. However, implementing mechanisms such as these in practice often comes with significant computational overhead and can expose potential security threats. Novel computing paradigms, such as analog, quantum, and specialized digital hardware, present opportunities for implementing privacy-preserving machine learning systems while enhancing security and mitigating performance loss. This work instantiates these ideas by applying the FHE scheme to a Federated Learning Neural Network architecture that integrates both classical and quantum layers.

AQ-PINNs: Attention-Enhanced Quantum Physics-Informed Neural Networks for Carbon-Efficient Climate Modeling

The growing computational demands of artificial intelligence (AI) in addressing climate change raise significant concerns about inefficiencies and environmental impact, as highlighted by the Jevons paradox. We propose an attention-enhanced quantum physics-informed neural networks model (AQ-PINNs) to tackle these challenges. This approach integrates quantum computing techniques into physics-informed neural networks (PINNs) for climate modeling, aiming to enhance predictive accuracy in fluid dynamics governed by the Navier-Stokes equations while reducing the computational burden and carbon footprint. By harnessing variational quantum multi-head self-attention mechanisms, our AQ-PINNs achieve a 51.51% reduction in model parameters compared to classical multi-head self-attention methods while maintaining comparable convergence and loss. It also employs quantum tensor networks to enhance representational capacity, which can lead to more efficient gradient computations and reduced susceptibility to barren plateaus. Our AQ-PINNs represent a crucial step towards more sustainable and effective climate modeling solutions.

QADQN: Quantum Attention Deep Q-Network for Financial Market Prediction

Financial market prediction and optimal trading strategy development remain challenging due to market complexity and volatility. Our research in quantum finance and reinforcement learning for decision-making demonstrates the approach of quantum-classical hybrid algorithms to tackling real-world financial challenges. In this respect, we corroborate the concept with rigorous backtesting and validate the framework's performance under realistic market conditions, by including fixed transaction cost per trade. This paper introduces a Quantum Attention Deep Q-Network (QADQN) approach to address these challenges through quantum-enhanced reinforcement learning. Our QADQN architecture uses a variational quantum circuit inside a traditional deep Q-learning framework to take advantage of possible quantum advantages in decision-making. We gauge the QADQN agent's performance on historical data from major market indices, including the S&P 500. We evaluate the agent's learning process by examining its reward accumulation and the effectiveness of its experience replay mechanism. Our empirical results demonstrate the QADQN's superior performance, achieving better risk-adjusted returns with Sortino ratios of 1.28 and 1.19 for non-overlapping and overlapping test periods respectively, indicating effective downside risk management.

Financial Fraud Detection using Quantum Graph Neural Networks

Financial fraud detection is essential for preventing significant financial losses and maintaining the reputation of financial institutions. However, conventional methods of detecting financial fraud have limited effectiveness, necessitating the need for new approaches to improve detection rates. In this paper, we propose a novel approach for detecting financial fraud using Quantum Graph Neural Networks (QGNNs). QGNNs are a type of neural network that can process graph-structured data and leverage the power of Quantum Computing (QC) to perform computations more efficiently than classical neural networks. Our approach uses Variational Quantum Circuits (VQC) to enhance the performance of the QGNN. In order to evaluate the efficiency of our proposed method, we compared the performance of QGNNs to Classical Graph Neural Networks using a real-world financial fraud detection dataset. The results of our experiments showed that QGNNs achieved an AUC of $0.85$, which outperformed classical GNNs. Our research highlights the potential of QGNNs and suggests that QGNNs are a promising new approach for improving financial fraud detection.