Luming Duan
An efficient quantum algorithm for generative machine learning
Nov 06, 2017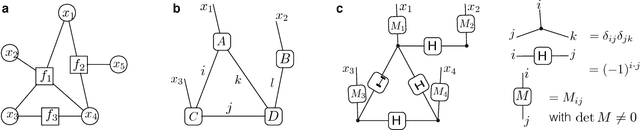
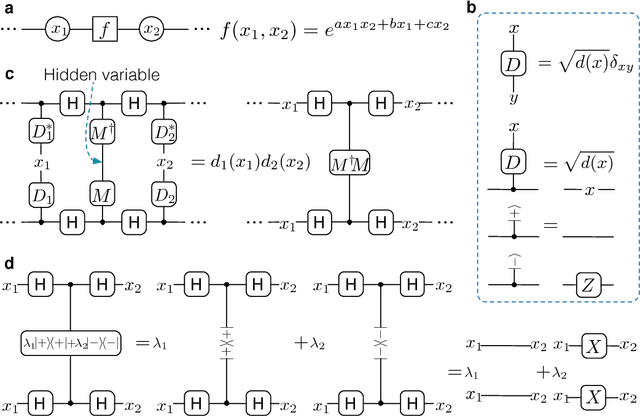
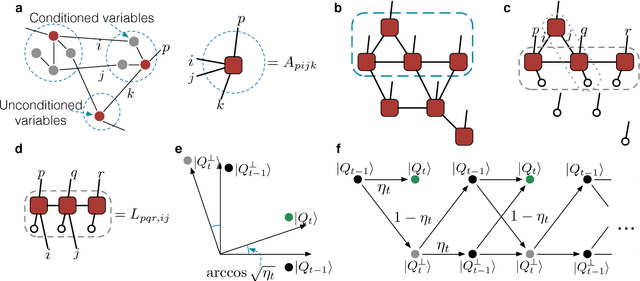
Abstract:A central task in the field of quantum computing is to find applications where quantum computer could provide exponential speedup over any classical computer. Machine learning represents an important field with broad applications where quantum computer may offer significant speedup. Several quantum algorithms for discriminative machine learning have been found based on efficient solving of linear algebraic problems, with potential exponential speedup in runtime under the assumption of effective input from a quantum random access memory. In machine learning, generative models represent another large class which is widely used for both supervised and unsupervised learning. Here, we propose an efficient quantum algorithm for machine learning based on a quantum generative model. We prove that our proposed model is exponentially more powerful to represent probability distributions compared with classical generative models and has exponential speedup in training and inference at least for some instances under a reasonable assumption in computational complexity theory. Our result opens a new direction for quantum machine learning and offers a remarkable example in which a quantum algorithm shows exponential improvement over any classical algorithm in an important application field.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge