Can Error Mitigation Improve Trainability of Noisy Variational Quantum Algorithms?

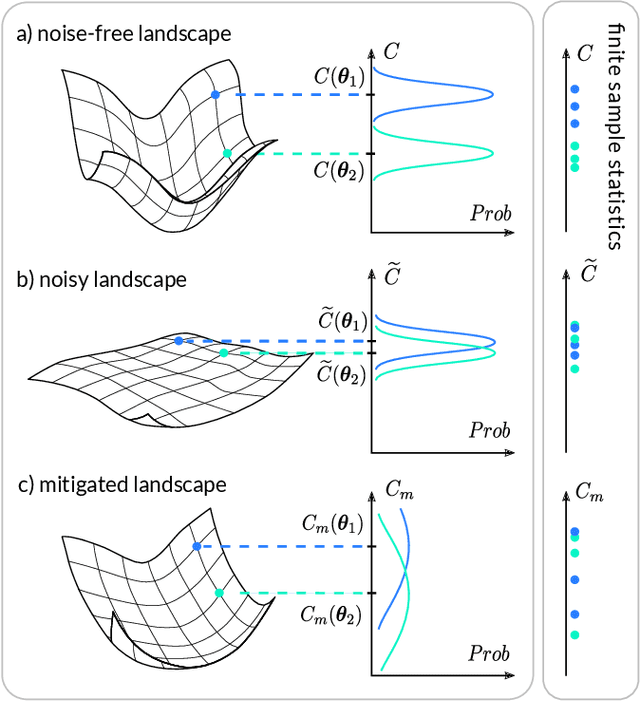
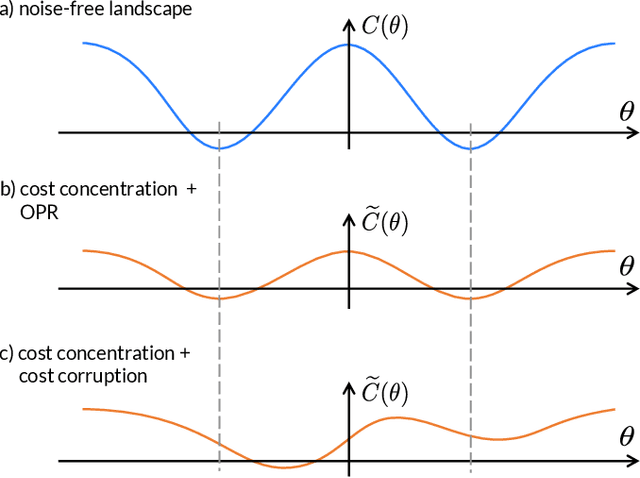
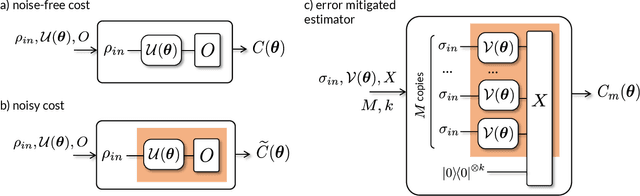
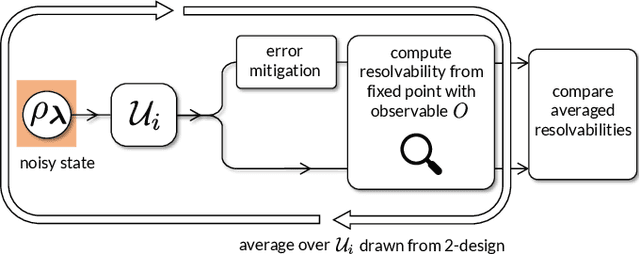
Variational Quantum Algorithms (VQAs) are widely viewed as the best hope for near-term quantum advantage. However, recent studies have shown that noise can severely limit the trainability of VQAs, e.g., by exponentially flattening the cost landscape and suppressing the magnitudes of cost gradients. Error Mitigation (EM) shows promise in reducing the impact of noise on near-term devices. Thus, it is natural to ask whether EM can improve the trainability of VQAs. In this work, we first show that, for a broad class of EM strategies, exponential cost concentration cannot be resolved without committing exponential resources elsewhere. This class of strategies includes as special cases Zero Noise Extrapolation, Virtual Distillation, Probabilistic Error Cancellation, and Clifford Data Regression. Second, we perform analytical and numerical analysis of these EM protocols, and we find that some of them (e.g., Virtual Distillation) can make it harder to resolve cost function values compared to running no EM at all. As a positive result, we do find numerical evidence that Clifford Data Regression (CDR) can aid the training process in certain settings where cost concentration is not too severe. Our results show that care should be taken in applying EM protocols as they can either worsen or not improve trainability. On the other hand, our positive results for CDR highlight the possibility of engineering error mitigation methods to improve trainability.

Effect of barren plateaus on gradient-free optimization

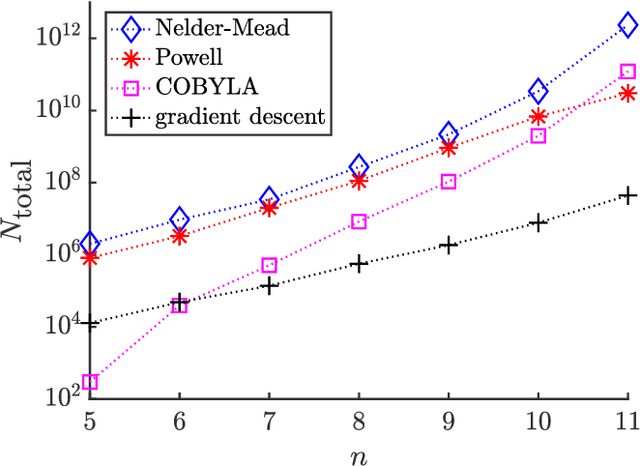
Barren plateau landscapes correspond to gradients that vanish exponentially in the number of qubits. Such landscapes have been demonstrated for variational quantum algorithms and quantum neural networks with either deep circuits or global cost functions. For obvious reasons, it is expected that gradient-based optimizers will be significantly affected by barren plateaus. However, whether or not gradient-free optimizers are impacted is a topic of debate, with some arguing that gradient-free approaches are unaffected by barren plateaus. Here we show that, indeed, gradient-free optimizers do not solve the barren plateau problem. Our main result proves that cost function differences, which are the basis for making decisions in a gradient-free optimization, are exponentially suppressed in a barren plateau. Hence, without exponential precision, gradient-free optimizers will not make progress in the optimization. We numerically confirm this by training in a barren plateau with several gradient-free optimizers (Nelder-Mead, Powell, and COBYLA algorithms), and show that the numbers of shots required in the optimization grows exponentially with the number of qubits.