Equivalence of quantum barren plateaus to cost concentration and narrow gorges

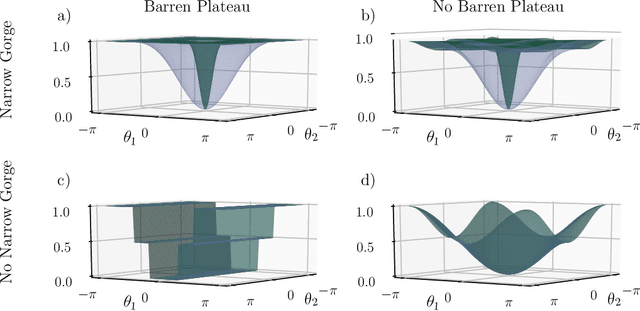
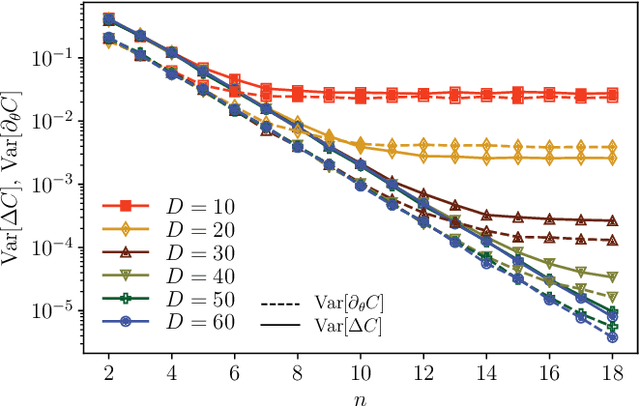
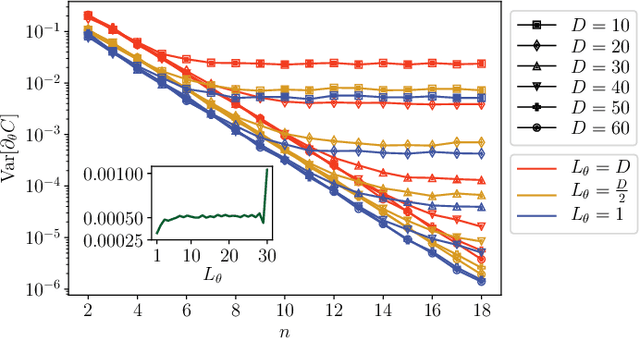
Optimizing parameterized quantum circuits (PQCs) is the leading approach to make use of near-term quantum computers. However, very little is known about the cost function landscape for PQCs, which hinders progress towards quantum-aware optimizers. In this work, we investigate the connection between three different landscape features that have been observed for PQCs: (1) exponentially vanishing gradients (called barren plateaus), (2) exponential cost concentration about the mean, and (3) the exponential narrowness of minina (called narrow gorges). We analytically prove that these three phenomena occur together, i.e., when one occurs then so do the other two. A key implication of this result is that one can numerically diagnose barren plateaus via cost differences rather than via the computationally more expensive gradients. More broadly, our work shows that quantum mechanics rules out certain cost landscapes (which otherwise would be mathematically possible), and hence our results are interesting from a quantum foundations perspective.