The effect of the number of parameters and the number of local feature patches on loss landscapes in distributed quantum neural networks

Quantum neural networks hold promise for tackling computationally challenging tasks that are intractable for classical computers. However, their practical application is hindered by significant optimization challenges, arising from complex loss landscapes characterized by barren plateaus and numerous local minima. These problems become more severe as the number of parameters or qubits increases, hampering effective training. To mitigate these optimization challenges, particularly for quantum machine learning applied to classical data, we employ an approach of distributing overlapping local patches across multiple quantum neural networks, processing each patch with an independent quantum neural network, and aggregating their outputs for prediction. In this study, we investigate how the number of parameters and patches affects the loss landscape geometry of this distributed quantum neural network architecture via Hessian analysis and loss landscape visualization. Our results confirm that increasing the number of parameters tends to lead to deeper and sharper loss landscapes. Crucially, we demonstrate that increasing the number of patches significantly reduces the largest Hessian eigenvalue at minima. This finding suggests that our distributed patch approach acts as a form of implicit regularization, promoting optimization stability and potentially enhancing generalization. Our study provides valuable insights into optimization challenges and highlights that the distributed patch approach is a promising strategy for developing more trainable and practical quantum machine learning models for classical data tasks.

Distributed Quantum Neural Networks via Partitioned Features Encoding

Quantum neural networks are expected to be a promising application in near-term quantum computing, but face challenges such as vanishing gradients during optimization and limited expressibility by a limited number of qubits and shallow circuits. To mitigate these challenges, an approach using distributed quantum neural networks has been proposed to make a prediction by approximating outputs of a large circuit using multiple small circuits. However, the approximation of a large circuit requires an exponential number of small circuit evaluations. Here, we instead propose to distribute partitioned features over multiple small quantum neural networks and use the ensemble of their expectation values to generate predictions. To verify our distributed approach, we demonstrate ten class classification of the Semeion and MNIST handwritten digit datasets. The results of the Semeion dataset imply that while our distributed approach may outperform a single quantum neural network in classification performance, excessive partitioning reduces performance. Nevertheless, for the MNIST dataset, we succeeded in ten class classification with exceeding 96\% accuracy. Our proposed method not only achieved highly accurate predictions for a large dataset but also reduced the hardware requirements for each quantum neural network compared to a large single quantum neural network. Our results highlight distributed quantum neural networks as a promising direction for practical quantum machine learning algorithms compatible with near-term quantum devices. We hope that our approach is useful for exploring quantum machine learning applications.

Quantum Kernel t-Distributed Stochastic Neighbor Embedding

Data visualization is important in understanding the characteristics of data that are difficult to see directly. It is used to visualize loss landscapes and optimization trajectories to analyze optimization performance. Popular optimization analysis is performed by visualizing a loss landscape around the reached local or global minimum using principal component analysis. However, this visualization depends on the variational parameters of a quantum circuit rather than quantum states, which makes it difficult to understand the mechanism of optimization process through the property of quantum states. Here, we propose a quantum data visualization method using quantum kernels, which enables us to offer fast and highly accurate visualization of quantum states. In our numerical experiments, we visualize hand-written digits dataset and apply $k$-nearest neighbor algorithm to the low-dimensional data to quantitatively evaluate our proposed method compared with a classical kernel method. As a result, our proposed method achieves comparable accuracy to the state-of-the-art classical kernel method, meaning that the proposed visualization method based on quantum machine learning does not degrade the separability of the input higher dimensional data. Furthermore, we visualize the optimization trajectories of finding the ground states of transverse field Ising model and successfully find the trajectory characteristics. Since quantum states are higher dimensional objects that can only be seen via observables, our visualization method, which inherits the similarity of quantum data, would be useful in understanding the behavior of quantum circuits and algorithms.

Parametric t-Stochastic Neighbor Embedding With Quantum Neural Network

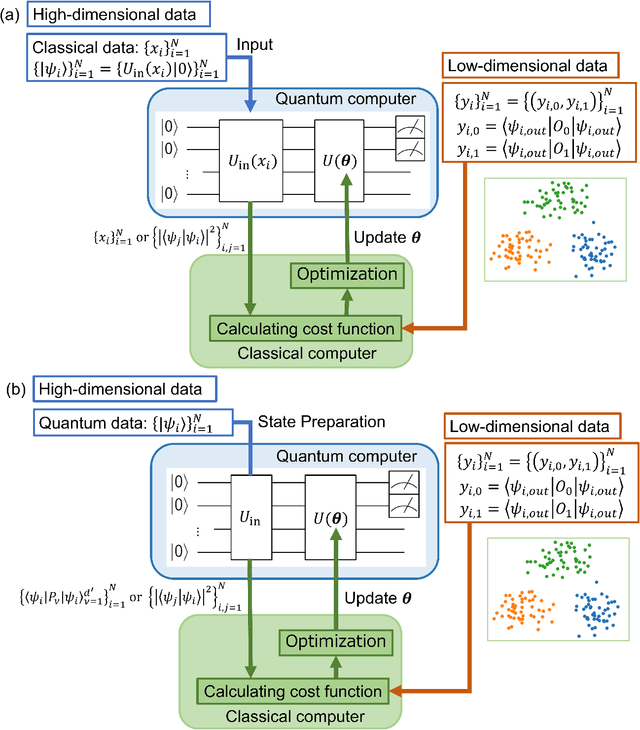
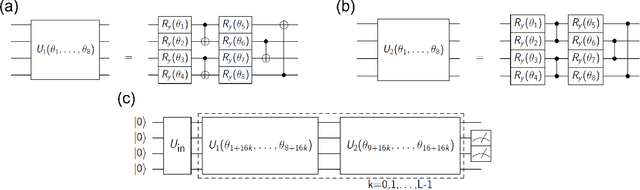
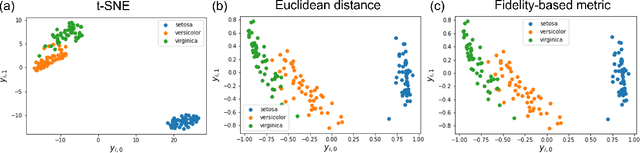
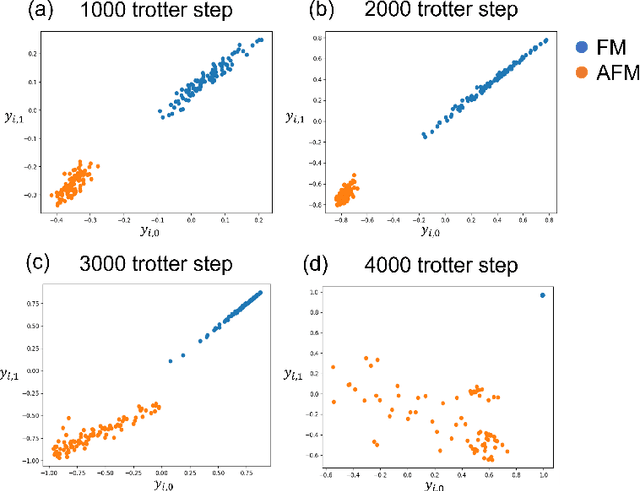
t-Stochastic Neighbor Embedding (t-SNE) is a non-parametric data visualization method in classical machine learning. It maps the data from the high-dimensional space into a low-dimensional space, especially a two-dimensional plane, while maintaining the relationship, or similarities, between the surrounding points. In t-SNE, the initial position of the low-dimensional data is randomly determined, and the visualization is achieved by moving the low-dimensional data to minimize a cost function. Its variant called parametric t-SNE uses neural networks for this mapping. In this paper, we propose to use quantum neural networks for parametric t-SNE to reflect the characteristics of high-dimensional quantum data on low-dimensional data. We use fidelity-based metrics instead of Euclidean distance in calculating high-dimensional data similarity. We visualize both classical (Iris dataset) and quantum (time-depending Hamiltonian dynamics) data for classification tasks. Since this method allows us to represent a quantum dataset in a higher dimensional Hilbert space by a quantum dataset in a lower dimension while keeping their similarity, the proposed method can also be used to compress quantum data for further quantum machine learning.