Power of data in quantum machine learning

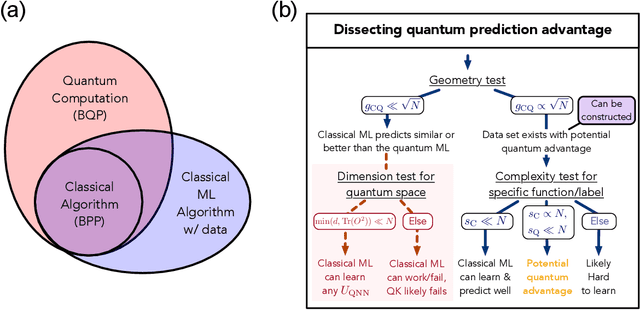
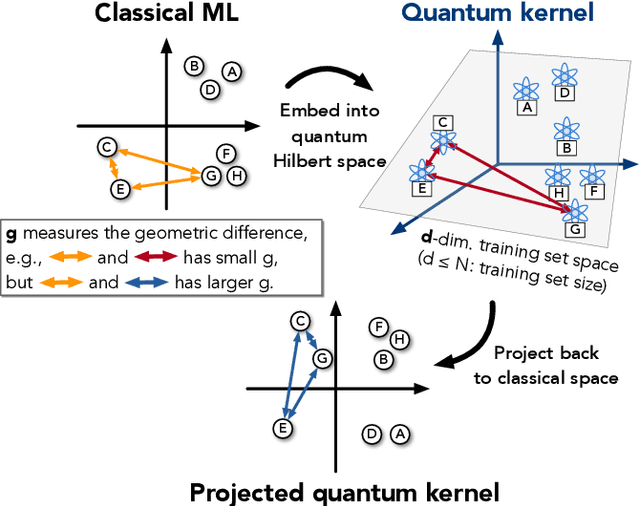
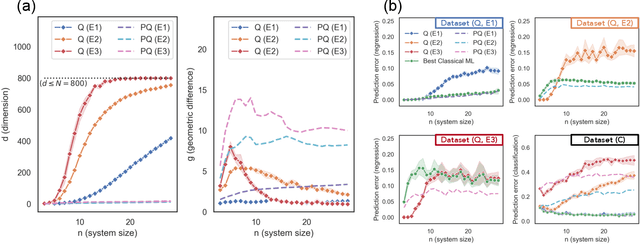
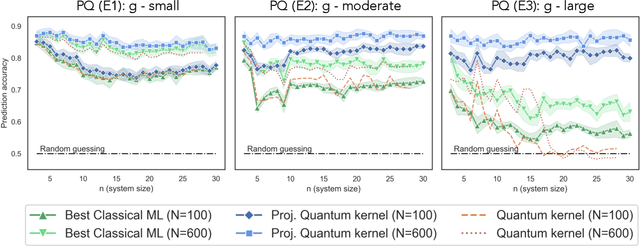
The use of quantum computing for machine learning is among the most exciting prospective applications of quantum technologies. At the crux of excitement is the potential for quantum computers to perform some computations exponentially faster than their classical counterparts. However, a machine learning task where some data is provided can be considerably different than more commonly studied computational tasks. In this work, we show that some problems that are classically hard to compute can be predicted easily with classical machines that learn from data. We find that classical machines can often compete or outperform existing quantum models even on data sets generated by quantum evolution, especially at large system sizes. Using rigorous prediction error bounds as a foundation, we develop a methodology for assessing the potential for quantum advantage in prediction on learning tasks. We show how the use of exponentially large quantum Hilbert space in existing quantum models can result in significantly inferior prediction performance compared to classical machines. To circumvent the observed setbacks, we propose an improvement by projecting all quantum states to an approximate classical representation. The projected quantum model provides a simple and rigorous quantum speed-up for a recently proposed learning problem in the fault-tolerant regime. For more near-term quantum models, the projected versions demonstrate a significant prediction advantage over some classical models on engineered data sets in one of the largest numerical tests for gate-based quantum machine learning to date, up to 30 qubits.