Learning quantum states prepared by shallow circuits in polynomial time

We give a polynomial time algorithm that, given copies of an unknown quantum state $\vert\psi\rangle=U\vert 0^n\rangle$ that is prepared by an unknown constant depth circuit $U$ on a finite-dimensional lattice, learns a constant depth quantum circuit that prepares $\vert\psi\rangle$. The algorithm extends to the case when the depth of $U$ is $\mathrm{polylog}(n)$, with a quasi-polynomial run-time. The key new idea is a simple and general procedure that efficiently reconstructs the global state $\vert\psi\rangle$ from its local reduced density matrices. As an application, we give an efficient algorithm to test whether an unknown quantum state on a lattice has low or high quantum circuit complexity.

Edge Classification on Graphs: New Directions in Topological Imbalance

Recent years have witnessed the remarkable success of applying Graph machine learning (GML) to node/graph classification and link prediction. However, edge classification task that enjoys numerous real-world applications such as social network analysis and cybersecurity, has not seen significant advancement. To address this gap, our study pioneers a comprehensive approach to edge classification. We identify a novel `Topological Imbalance Issue', which arises from the skewed distribution of edges across different classes, affecting the local subgraph of each edge and harming the performance of edge classifications. Inspired by the recent studies in node classification that the performance discrepancy exists with varying local structural patterns, we aim to investigate if the performance discrepancy in topological imbalanced edge classification can also be mitigated by characterizing the local class distribution variance. To overcome this challenge, we introduce Topological Entropy (TE), a novel topological-based metric that measures the topological imbalance for each edge. Our empirical studies confirm that TE effectively measures local class distribution variance, and indicate that prioritizing edges with high TE values can help address the issue of topological imbalance. Based on this, we develop two strategies - Topological Reweighting and TE Wedge-based Mixup - to focus training on (synthetic) edges based on their TEs. While topological reweighting directly manipulates training edge weights according to TE, our wedge-based mixup interpolates synthetic edges between high TE wedges. Ultimately, we integrate these strategies into a novel topological imbalance strategy for edge classification: TopoEdge. Through extensive experiments, we demonstrate the efficacy of our proposed strategies on newly curated datasets and thus establish a new benchmark for (imbalanced) edge classification.

Learning shallow quantum circuits

Despite fundamental interests in learning quantum circuits, the existence of a computationally efficient algorithm for learning shallow quantum circuits remains an open question. Because shallow quantum circuits can generate distributions that are classically hard to sample from, existing learning algorithms do not apply. In this work, we present a polynomial-time classical algorithm for learning the description of any unknown $n$-qubit shallow quantum circuit $U$ (with arbitrary unknown architecture) within a small diamond distance using single-qubit measurement data on the output states of $U$. We also provide a polynomial-time classical algorithm for learning the description of any unknown $n$-qubit state $\lvert \psi \rangle = U \lvert 0^n \rangle$ prepared by a shallow quantum circuit $U$ (on a 2D lattice) within a small trace distance using single-qubit measurements on copies of $\lvert \psi \rangle$. Our approach uses a quantum circuit representation based on local inversions and a technique to combine these inversions. This circuit representation yields an optimization landscape that can be efficiently navigated and enables efficient learning of quantum circuits that are classically hard to simulate.

A Topological Perspective on Demystifying GNN-Based Link Prediction Performance

Graph Neural Networks (GNNs) have shown great promise in learning node embeddings for link prediction (LP). While numerous studies aim to improve the overall LP performance of GNNs, none have explored its varying performance across different nodes and its underlying reasons. To this end, we aim to demystify which nodes will perform better from the perspective of their local topology. Despite the widespread belief that low-degree nodes exhibit poorer LP performance, our empirical findings provide nuances to this viewpoint and prompt us to propose a better metric, Topological Concentration (TC), based on the intersection of the local subgraph of each node with the ones of its neighbors. We empirically demonstrate that TC has a higher correlation with LP performance than other node-level topological metrics like degree and subgraph density, offering a better way to identify low-performing nodes than using cold-start. With TC, we discover a novel topological distribution shift issue in which newly joined neighbors of a node tend to become less interactive with that node's existing neighbors, compromising the generalizability of node embeddings for LP at testing time. To make the computation of TC scalable, We further propose Approximated Topological Concentration (ATC) and theoretically/empirically justify its efficacy in approximating TC and reducing the computation complexity. Given the positive correlation between node TC and its LP performance, we explore the potential of boosting LP performance via enhancing TC by re-weighting edges in the message-passing and discuss its effectiveness with limitations. Our code is publicly available at https://github.com/YuWVandy/Topo_LP_GNN.

Fairness and Diversity in Recommender Systems: A Survey

Recommender systems are effective tools for mitigating information overload and have seen extensive applications across various domains. However, the single focus on utility goals proves to be inadequate in addressing real-world concerns, leading to increasing attention to fairness-aware and diversity-aware recommender systems. While most existing studies explore fairness and diversity independently, we identify strong connections between these two domains. In this survey, we first discuss each of them individually and then dive into their connections. Additionally, motivated by the concepts of user-level and item-level fairness, we broaden the understanding of diversity to encompass not only the item level but also the user level. With this expanded perspective on user and item-level diversity, we re-interpret fairness studies from the viewpoint of diversity. This fresh perspective enhances our understanding of fairness-related work and paves the way for potential future research directions. Papers discussed in this survey along with public code links are available at https://github.com/YuyingZhao/Awesome-Fairness-and-Diversity-Papers-in-Recommender-Systems .

A rigorous and robust quantum speed-up in supervised machine learning

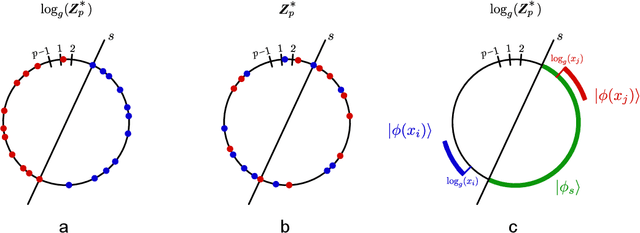
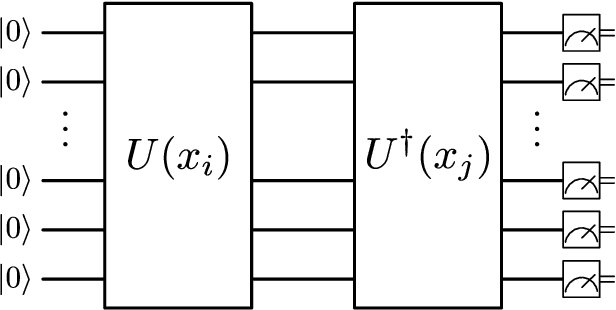
Over the past few years several quantum machine learning algorithms were proposed that promise quantum speed-ups over their classical counterparts. Most of these learning algorithms assume quantum access to data; and it is unclear if quantum speed-ups still exist without making these strong assumptions. In this paper, we establish a rigorous quantum speed-up for supervised classification using a quantum learning algorithm that only requires classical access to data. Our quantum classifier is a conventional support vector machine that uses a fault-tolerant quantum computer to estimate a kernel function. Data samples are mapped to a quantum feature space and the kernel entries can be estimated as the transition amplitude of a quantum circuit. We construct a family of datasets and show that no classical learner can classify the data inverse-polynomially better than random guessing, assuming the widely-believed hardness of the discrete logarithm problem. Meanwhile, the quantum classifier achieves high accuracy and is robust against additive errors in the kernel entries that arise from finite sampling statistics.