A rigorous and robust quantum speed-up in supervised machine learning

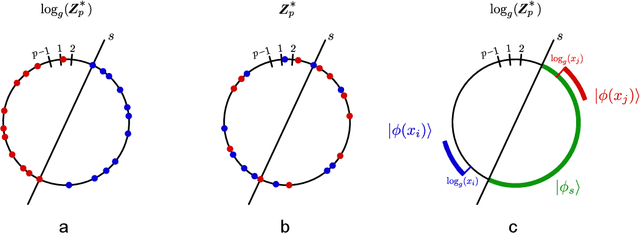
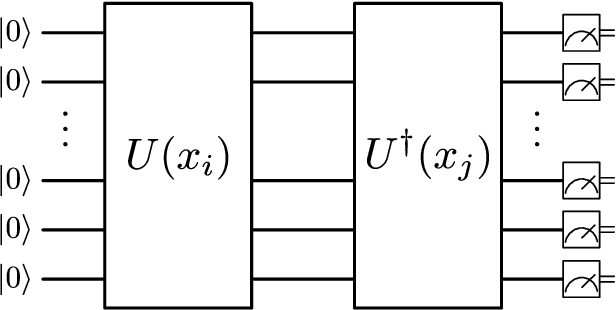
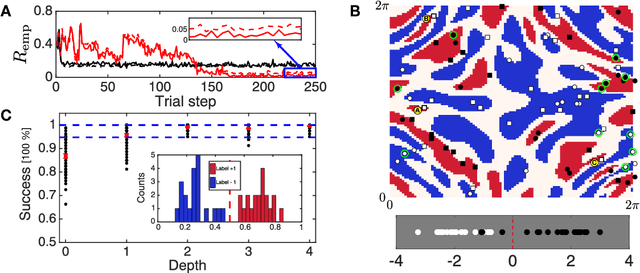
Over the past few years several quantum machine learning algorithms were proposed that promise quantum speed-ups over their classical counterparts. Most of these learning algorithms assume quantum access to data; and it is unclear if quantum speed-ups still exist without making these strong assumptions. In this paper, we establish a rigorous quantum speed-up for supervised classification using a quantum learning algorithm that only requires classical access to data. Our quantum classifier is a conventional support vector machine that uses a fault-tolerant quantum computer to estimate a kernel function. Data samples are mapped to a quantum feature space and the kernel entries can be estimated as the transition amplitude of a quantum circuit. We construct a family of datasets and show that no classical learner can classify the data inverse-polynomially better than random guessing, assuming the widely-believed hardness of the discrete logarithm problem. Meanwhile, the quantum classifier achieves high accuracy and is robust against additive errors in the kernel entries that arise from finite sampling statistics.

Supervised learning with quantum enhanced feature spaces

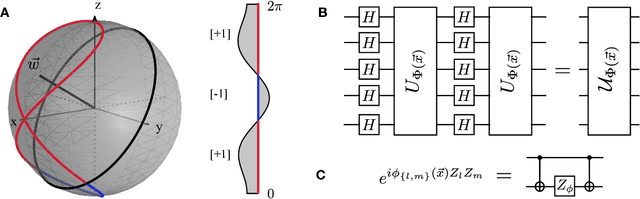
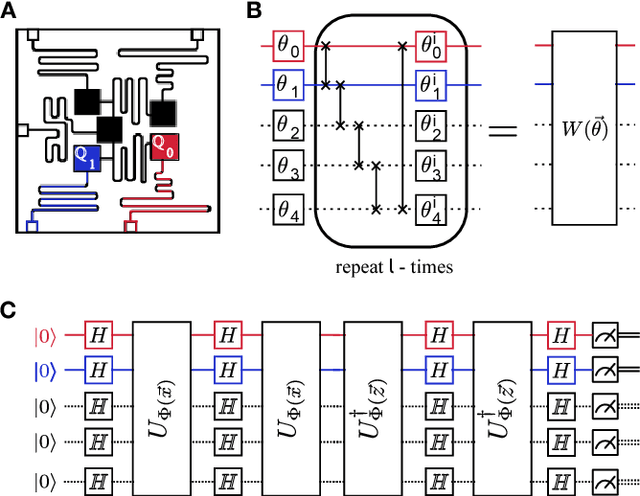
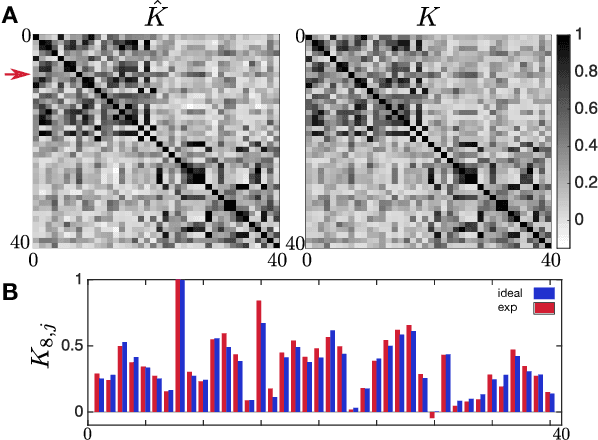
Machine learning and quantum computing are two technologies each with the potential for altering how computation is performed to address previously untenable problems. Kernel methods for machine learning are ubiquitous for pattern recognition, with support vector machines (SVMs) being the most well-known method for classification problems. However, there are limitations to the successful solution to such problems when the feature space becomes large, and the kernel functions become computationally expensive to estimate. A core element to computational speed-ups afforded by quantum algorithms is the exploitation of an exponentially large quantum state space through controllable entanglement and interference. Here, we propose and experimentally implement two novel methods on a superconducting processor. Both methods represent the feature space of a classification problem by a quantum state, taking advantage of the large dimensionality of quantum Hilbert space to obtain an enhanced solution. One method, the quantum variational classifier builds on [1,2] and operates through using a variational quantum circuit to classify a training set in direct analogy to conventional SVMs. In the second, a quantum kernel estimator, we estimate the kernel function and optimize the classifier directly. The two methods present a new class of tools for exploring the applications of noisy intermediate scale quantum computers [3] to machine learning.