Provably efficient variational generative modeling of quantum many-body systems via quantum-probabilistic information geometry

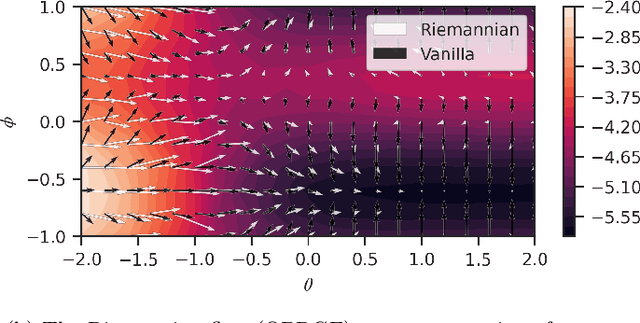
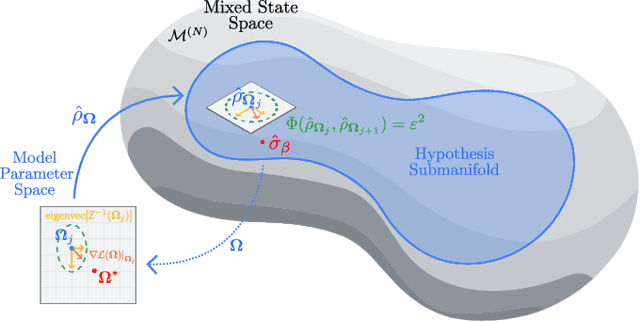
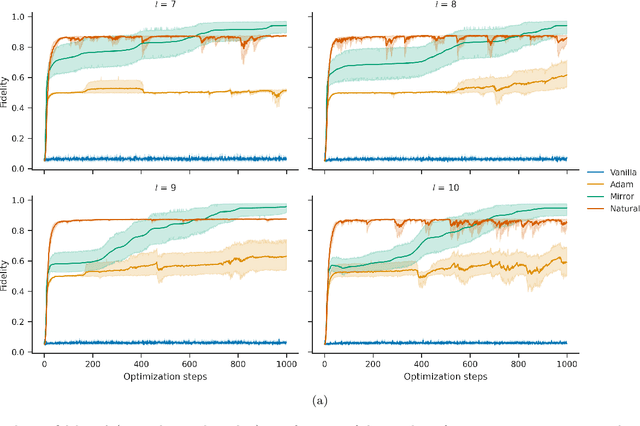
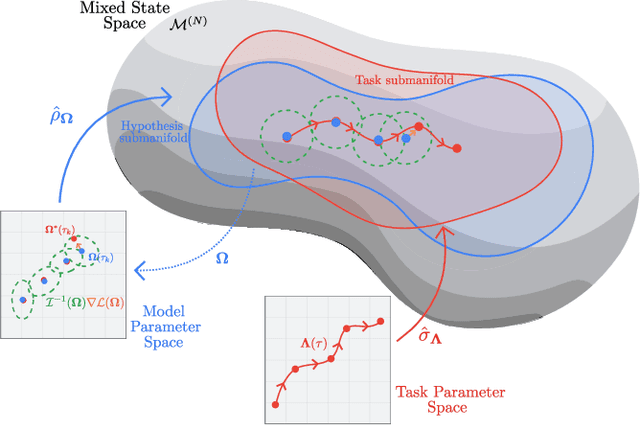
The dual tasks of quantum Hamiltonian learning and quantum Gibbs sampling are relevant to many important problems in physics and chemistry. In the low temperature regime, algorithms for these tasks often suffer from intractabilities, for example from poor sample- or time-complexity. With the aim of addressing such intractabilities, we introduce a generalization of quantum natural gradient descent to parameterized mixed states, as well as provide a robust first-order approximating algorithm, Quantum-Probabilistic Mirror Descent. We prove data sample efficiency for the dual tasks using tools from information geometry and quantum metrology, thus generalizing the seminal result of classical Fisher efficiency to a variational quantum algorithm for the first time. Our approaches extend previously sample-efficient techniques to allow for flexibility in model choice, including to spectrally-decomposed models like Quantum Hamiltonian-Based Models, which may circumvent intractable time complexities. Our first-order algorithm is derived using a novel quantum generalization of the classical mirror descent duality. Both results require a special choice of metric, namely, the Bogoliubov-Kubo-Mori metric. To test our proposed algorithms numerically, we compare their performance to existing baselines on the task of quantum Gibbs sampling for the transverse field Ising model. Finally, we propose an initialization strategy leveraging geometric locality for the modelling of sequences of states such as those arising from quantum-stochastic processes. We demonstrate its effectiveness empirically for both real and imaginary time evolution while defining a broader class of potential applications.

Group-Invariant Quantum Machine Learning

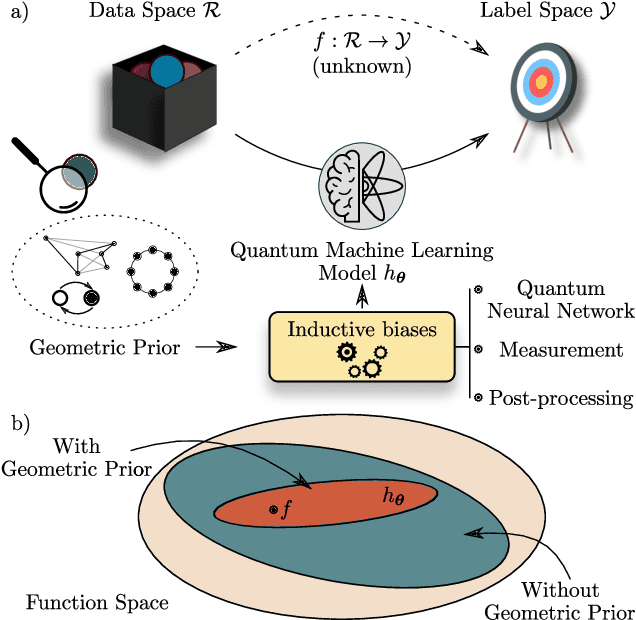
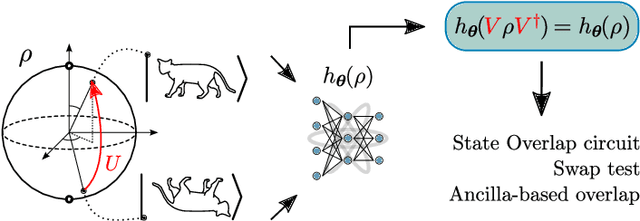
Quantum Machine Learning (QML) models are aimed at learning from data encoded in quantum states. Recently, it has been shown that models with little to no inductive biases (i.e., with no assumptions about the problem embedded in the model) are likely to have trainability and generalization issues, especially for large problem sizes. As such, it is fundamental to develop schemes that encode as much information as available about the problem at hand. In this work we present a simple, yet powerful, framework where the underlying invariances in the data are used to build QML models that, by construction, respect those symmetries. These so-called group-invariant models produce outputs that remain invariant under the action of any element of the symmetry group $\mathfrak{G}$ associated to the dataset. We present theoretical results underpinning the design of $\mathfrak{G}$-invariant models, and exemplify their application through several paradigmatic QML classification tasks including cases when $\mathfrak{G}$ is a continuous Lie group and also when it is a discrete symmetry group. Notably, our framework allows us to recover, in an elegant way, several well known algorithms for the literature, as well as to discover new ones. Taken together, we expect that our results will help pave the way towards a more geometric and group-theoretic approach to QML model design.