Group-Invariant Quantum Machine Learning
Paper and Code
May 04, 2022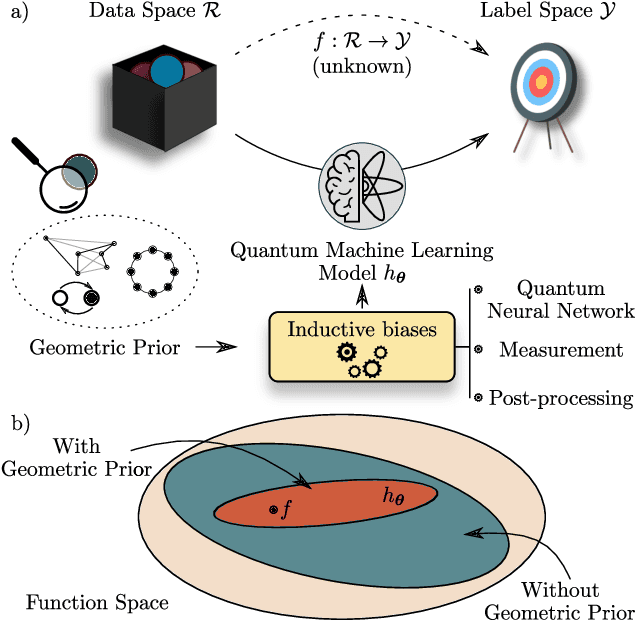

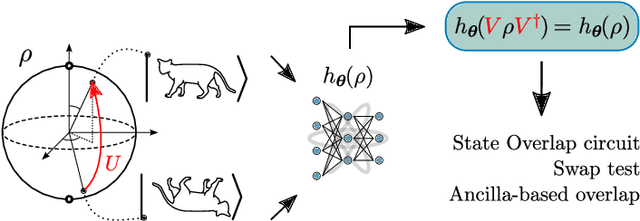
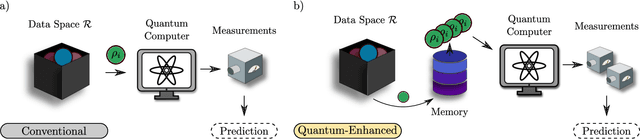
Quantum Machine Learning (QML) models are aimed at learning from data encoded in quantum states. Recently, it has been shown that models with little to no inductive biases (i.e., with no assumptions about the problem embedded in the model) are likely to have trainability and generalization issues, especially for large problem sizes. As such, it is fundamental to develop schemes that encode as much information as available about the problem at hand. In this work we present a simple, yet powerful, framework where the underlying invariances in the data are used to build QML models that, by construction, respect those symmetries. These so-called group-invariant models produce outputs that remain invariant under the action of any element of the symmetry group $\mathfrak{G}$ associated to the dataset. We present theoretical results underpinning the design of $\mathfrak{G}$-invariant models, and exemplify their application through several paradigmatic QML classification tasks including cases when $\mathfrak{G}$ is a continuous Lie group and also when it is a discrete symmetry group. Notably, our framework allows us to recover, in an elegant way, several well known algorithms for the literature, as well as to discover new ones. Taken together, we expect that our results will help pave the way towards a more geometric and group-theoretic approach to QML model design.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge