Exponential concentration and untrainability in quantum kernel methods
Paper and Code
Aug 23, 2022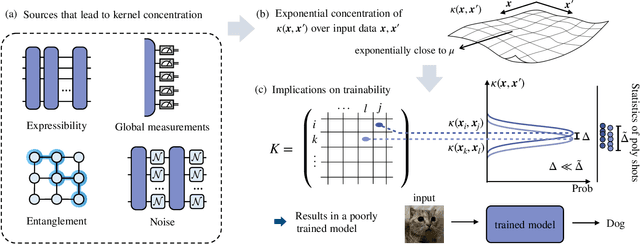
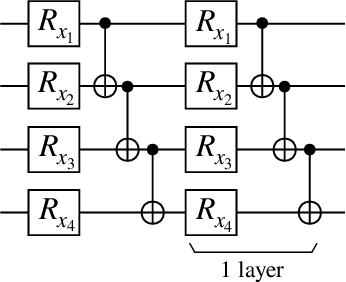
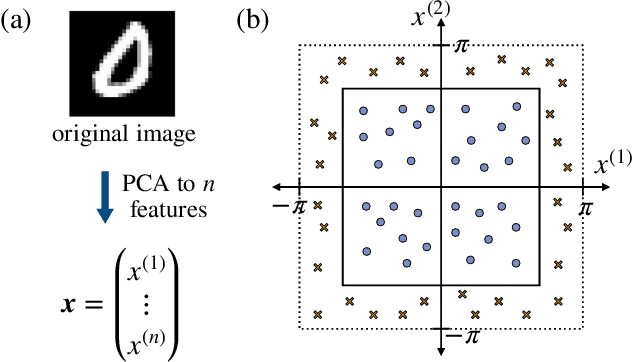
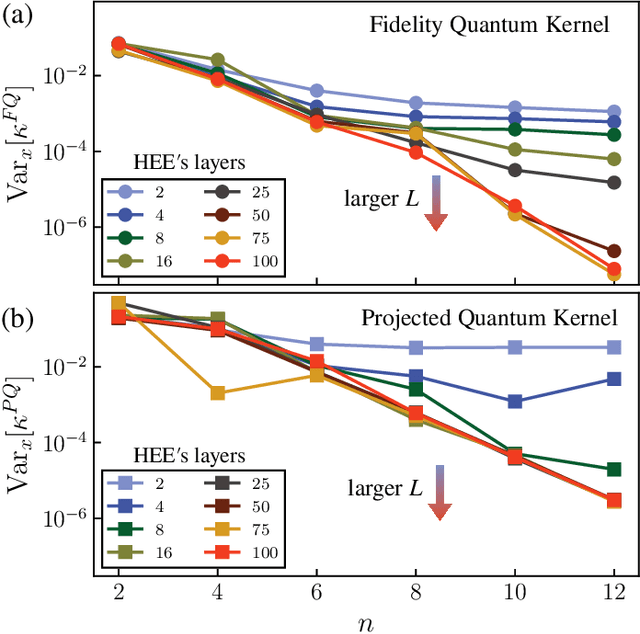
Kernel methods in Quantum Machine Learning (QML) have recently gained significant attention as a potential candidate for achieving a quantum advantage in data analysis. Among other attractive properties, when training a kernel-based model one is guaranteed to find the optimal model's parameters due to the convexity of the training landscape. However, this is based on the assumption that the quantum kernel can be efficiently obtained from a quantum hardware. In this work we study the trainability of quantum kernels from the perspective of the resources needed to accurately estimate kernel values. We show that, under certain conditions, values of quantum kernels over different input data can be exponentially concentrated (in the number of qubits) towards some fixed value, leading to an exponential scaling of the number of measurements required for successful training. We identify four sources that can lead to concentration including: the expressibility of data embedding, global measurements, entanglement and noise. For each source, an associated concentration bound of quantum kernels is analytically derived. Lastly, we show that when dealing with classical data, training a parametrized data embedding with a kernel alignment method is also susceptible to exponential concentration. Our results are verified through numerical simulations for several QML tasks. Altogether, we provide guidelines indicating that certain features should be avoided to ensure the efficient evaluation and the trainability of quantum kernel methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge