Beyond Ansätze: Learning Quantum Circuits as Unitary Operators

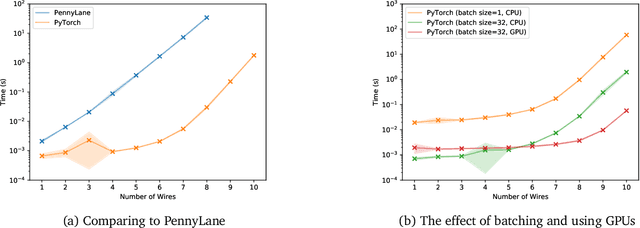
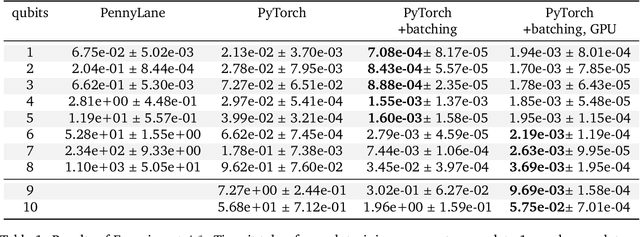
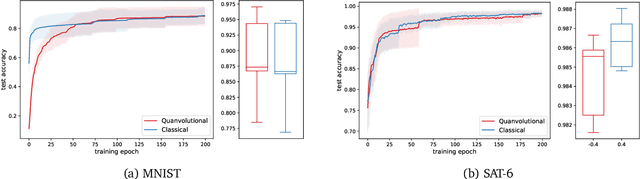
This paper explores the advantages of optimizing quantum circuits on $N$ wires as operators in the unitary group $U(2^N)$. We run gradient-based optimization in the Lie algebra $\mathfrak u(2^N)$ and use the exponential map to parametrize unitary matrices. We argue that $U(2^N)$ is not only more general than the search space induced by an ansatz, but in ways easier to work with on classical computers. The resulting approach is quick, ansatz-free and provides an upper bound on performance over all ans\"atze on $N$ wires.