Solvation Free Energies from Neural Thermodynamic Integration

We propose to compute solvation free energies via thermodynamic integration along a neural-network potential interpolating between two target Hamiltonians. We use a stochastic interpolant to define an interpolation between the distributions at the level of samples and optimize a neural network potential to match the corresponding equilibrium potential at every intermediate time-step. Once the alignment between the interpolating samples and the interpolating potentials is sufficiently accurate, the free-energy difference between the two Hamiltonians can be estimated using (neural) thermodynamic integration. We validate our method to compute solvation free energies on several benchmark systems: a Lennard-Jones particle in a Lennard-Jones fluid, as well as the insertion of both water and methane solutes in a water solvent at atomistic resolution.

Neural Thermodynamic Integration: Free Energies from Energy-based Diffusion Models

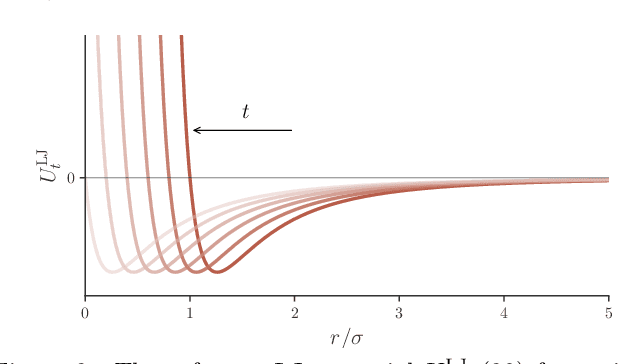
Thermodynamic integration (TI) offers a rigorous method for estimating free-energy differences by integrating over a sequence of interpolating conformational ensembles. However, TI calculations are computationally expensive and typically limited to coupling a small number of degrees of freedom due to the need to sample numerous intermediate ensembles with sufficient conformational-space overlap. In this work, we propose to perform TI along an alchemical pathway represented by a trainable neural network, which we term Neural TI. Critically, we parametrize a time-dependent Hamiltonian interpolating between the interacting and non-interacting systems, and optimize its gradient using a denoising-diffusion objective. The ability of the resulting energy-based diffusion model to sample all intermediate ensembles, allows us to perform TI from a single reference calculation. We apply our method to Lennard-Jones fluids, where we report accurate calculations of the excess chemical potential, demonstrating that Neural TI is capable of coupling hundreds of degrees of freedom at once.

Interpretable Embeddings From Molecular Simulations Using Gaussian Mixture Variational Autoencoders

Extracting insight from the enormous quantity of data generated from molecular simulations requires the identification of a small number of collective variables whose corresponding low-dimensional free-energy landscape retains the essential features of the underlying system. Data-driven techniques provide a systematic route to constructing this landscape, without the need for extensive a priori intuition into the relevant driving forces. In particular, autoencoders are powerful tools for dimensionality reduction, as they naturally force an information bottleneck and, thereby, a low-dimensional embedding of the essential features. While variational autoencoders ensure continuity of the embedding by assuming a unimodal Gaussian prior, this is at odds with the multi-basin free-energy landscapes that typically arise from the identification of meaningful collective variables. In this work, we incorporate this physical intuition into the prior by employing a Gaussian mixture variational autoencoder (GMVAE), which encourages the separation of metastable states within the embedding. The GMVAE performs dimensionality reduction and clustering within a single unified framework, and is capable of identifying the inherent dimensionality of the input data, in terms of the number of Gaussians required to categorize the data. We illustrate our approach on two toy models, alanine dipeptide, and a challenging disordered peptide ensemble, demonstrating the enhanced clustering effect of the GMVAE prior compared to standard VAEs. The resulting embeddings appear to be promising representations for constructing Markov state models, highlighting the transferability of the dimensionality reduction from static equilibrium properties to dynamics.