Thinking Slow, Fast: Scaling Inference Compute with Distilled Reasoners

Recent advancements have demonstrated that the performance of large language models (LLMs) can be significantly enhanced by scaling computational resources at test time. A common strategy involves generating multiple Chain-of-Thought (CoT) trajectories and aggregating their outputs through various selection mechanisms. This raises a fundamental question: can models with lower complexity leverage their superior generation throughput to outperform similarly sized Transformers for a fixed computational budget? To address this question and overcome the lack of strong subquadratic reasoners, we distill pure and hybrid Mamba models from pretrained Transformers. Trained on only 8 billion tokens, our distilled models show strong performance and scaling on mathematical reasoning datasets while being much faster at inference for large batches and long sequences. Despite the zero-shot performance hit due to distillation, both pure and hybrid Mamba models can scale their coverage and accuracy performance past their Transformer teacher models under fixed time budgets, opening a new direction for scaling inference compute.

Leveraging the true depth of LLMs

Large Language Models demonstrate remarkable capabilities at the cost of high compute requirements. While recent research has shown that intermediate layers can be removed or have their order shuffled without impacting performance significantly, these findings have not been employed to reduce the computational cost of inference. We investigate several potential ways to reduce the depth of pre-trained LLMs without significantly affecting performance. Leveraging our insights, we present a novel approach that exploits this decoupling between layers by grouping some of them into pairs that can be evaluated in parallel. This modification of the computational graph -- through better parallelism -- results in an average improvement of around 1.20x on the number of tokens generated per second, without re-training nor fine-tuning, while retaining 95%-99% of the original accuracy. Empirical evaluation demonstrates that this approach significantly improves serving efficiency while maintaining model performance, offering a practical improvement for large-scale LLM deployment.

The AdEMAMix Optimizer: Better, Faster, Older

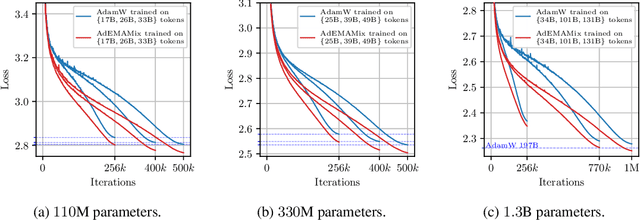
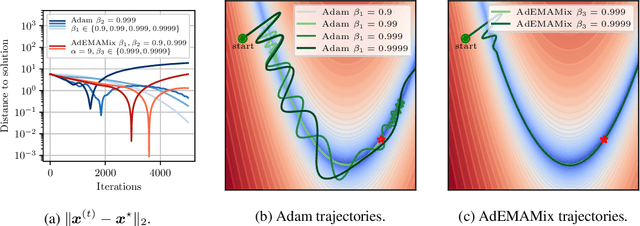
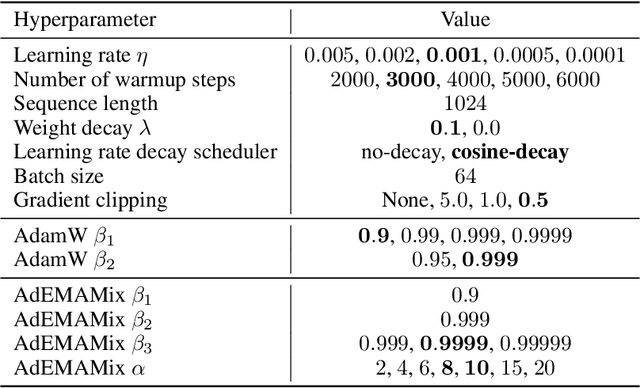
Momentum based optimizers are central to a wide range of machine learning applications. These typically rely on an Exponential Moving Average (EMA) of gradients, which decays exponentially the present contribution of older gradients. This accounts for gradients being local linear approximations which lose their relevance as the iterate moves along the loss landscape. This work questions the use of a single EMA to accumulate past gradients and empirically demonstrates how this choice can be sub-optimal: a single EMA cannot simultaneously give a high weight to the immediate past, and a non-negligible weight to older gradients. Building on this observation, we propose AdEMAMix, a simple modification of the Adam optimizer with a mixture of two EMAs to better take advantage of past gradients. Our experiments on language modeling and image classification show -- quite surprisingly -- that gradients can stay relevant for tens of thousands of steps. They help to converge faster, and often to lower minima: e.g., a $1.3$B parameter AdEMAMix LLM trained on $101$B tokens performs comparably to an AdamW model trained on $197$B tokens ($+95\%$). Moreover, our method significantly slows-down model forgetting during training. Our work motivates further exploration of different types of functions to leverage past gradients, beyond EMAs.

DenseFormer: Enhancing Information Flow in Transformers via Depth Weighted Averaging

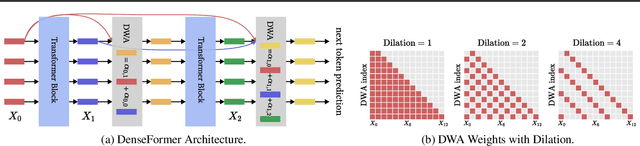
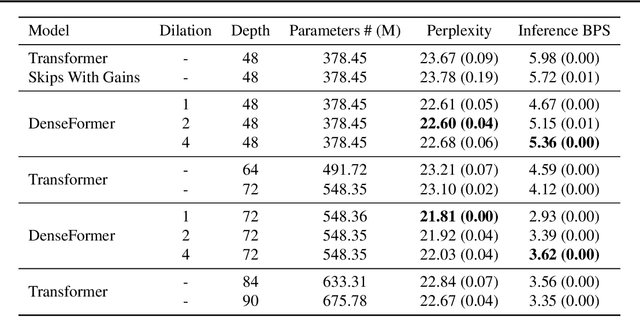
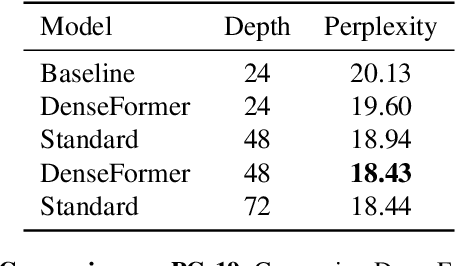
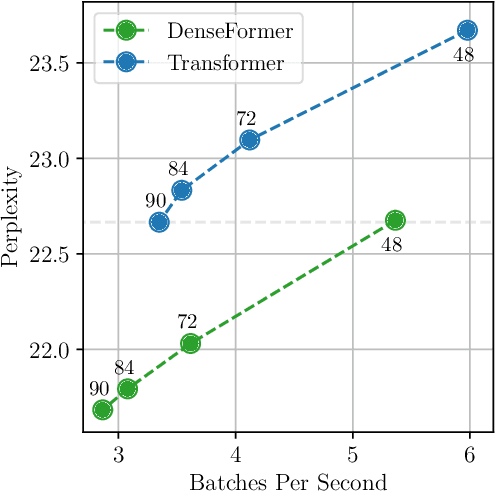
The transformer architecture from Vaswani et al. (2017) is now ubiquitous across application domains, from natural language processing to speech processing and image understanding. We propose DenseFormer, a simple modification to the standard architecture that improves the perplexity of the model without increasing its size -- adding a few thousand parameters for large-scale models in the 100B parameters range. Our approach relies on an additional averaging step after each transformer block, which computes a weighted average of current and past representations -- we refer to this operation as Depth-Weighted-Average (DWA). The learned DWA weights exhibit coherent patterns of information flow, revealing the strong and structured reuse of activations from distant layers. Experiments demonstrate that DenseFormer is more data efficient, reaching the same perplexity of much deeper transformer models, and that for the same perplexity, these new models outperform transformer baselines in terms of memory efficiency and inference time.

MEDITRON-70B: Scaling Medical Pretraining for Large Language Models

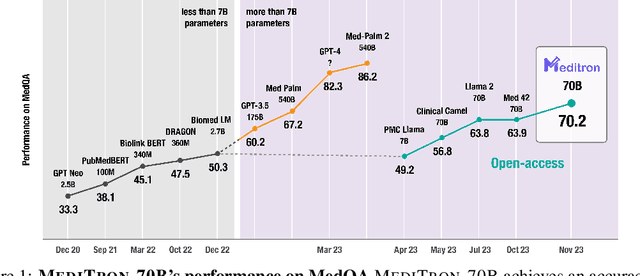
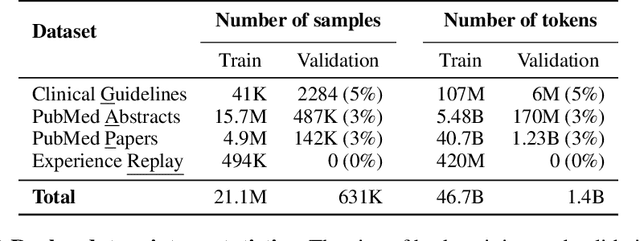
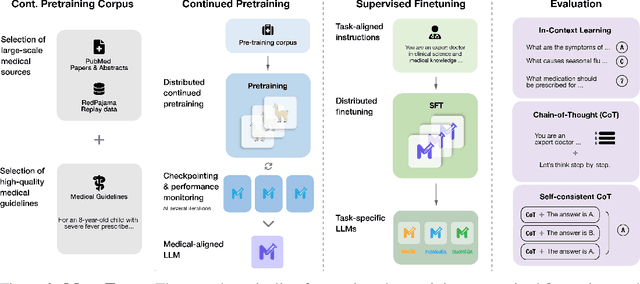
Large language models (LLMs) can potentially democratize access to medical knowledge. While many efforts have been made to harness and improve LLMs' medical knowledge and reasoning capacities, the resulting models are either closed-source (e.g., PaLM, GPT-4) or limited in scale (<= 13B parameters), which restricts their abilities. In this work, we improve access to large-scale medical LLMs by releasing MEDITRON: a suite of open-source LLMs with 7B and 70B parameters adapted to the medical domain. MEDITRON builds on Llama-2 (through our adaptation of Nvidia's Megatron-LM distributed trainer), and extends pretraining on a comprehensively curated medical corpus, including selected PubMed articles, abstracts, and internationally-recognized medical guidelines. Evaluations using four major medical benchmarks show significant performance gains over several state-of-the-art baselines before and after task-specific finetuning. Overall, MEDITRON achieves a 6% absolute performance gain over the best public baseline in its parameter class and 3% over the strongest baseline we finetuned from Llama-2. Compared to closed-source LLMs, MEDITRON-70B outperforms GPT-3.5 and Med-PaLM and is within 5% of GPT-4 and 10% of Med-PaLM-2. We release our code for curating the medical pretraining corpus and the MEDITRON model weights to drive open-source development of more capable medical LLMs.

DoGE: Domain Reweighting with Generalization Estimation

The coverage and composition of the pretraining data corpus significantly impacts the generalization ability of large language models. Conventionally, the pretraining corpus is composed of various source domains (e.g. CommonCrawl, Wikipedia, Github etc.) according to certain sampling probabilities (domain weights). However, current methods lack a principled way to optimize domain weights for ultimate goal for generalization. We propose DOmain reweighting with Generalization Estimation (DoGE), where we reweigh the sampling probability from each domain based on its contribution to the final generalization objective assessed by a gradient-based generalization estimation function. First, we train a small-scale proxy model with a min-max optimization to obtain the reweighted domain weights. At each step, the domain weights are updated to maximize the overall generalization gain by mirror descent. Finally we use the obtained domain weights to train a larger scale full-size language model. On SlimPajama-6B dataset, with universal generalization objective, DoGE achieves better average perplexity and zero-shot reasoning accuracy. On out-of-domain generalization tasks, DoGE reduces perplexity on the target domain by a large margin. We further apply a parameter-selection scheme which improves the efficiency of generalization estimation.

CoTFormer: More Tokens With Attention Make Up For Less Depth

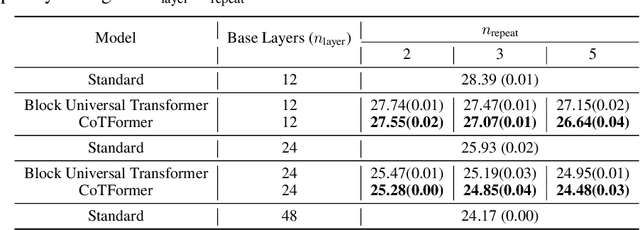
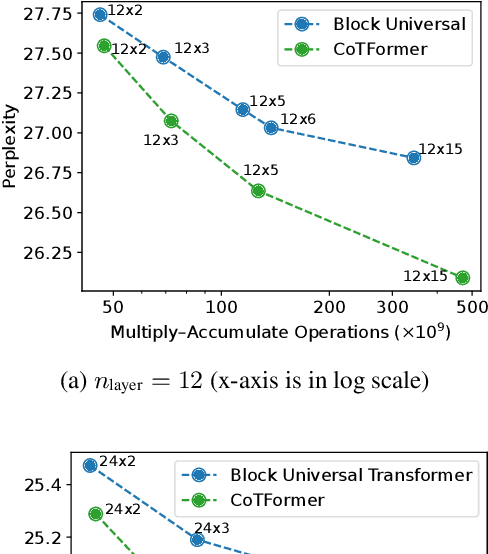
The race to continually develop ever larger and deeper foundational models is underway. However, techniques like the Chain-of-Thought (CoT) method continue to play a pivotal role in achieving optimal downstream performance. In this work, we establish an approximate parallel between using chain-of-thought and employing a deeper transformer. Building on this insight, we introduce CoTFormer, a transformer variant that employs an implicit CoT-like mechanism to achieve capacity comparable to a deeper model. Our empirical findings demonstrate the effectiveness of CoTFormers, as they significantly outperform larger standard transformers.

Faster Causal Attention Over Large Sequences Through Sparse Flash Attention

Transformer-based language models have found many diverse applications requiring them to process sequences of increasing length. For these applications, the causal self-attention -- which is the only component scaling quadratically w.r.t. the sequence length -- becomes a central concern. While many works have proposed schemes to sparsify the attention patterns and reduce the computational overhead of self-attention, those are often limited by implementations concerns and end up imposing a simple and static structure over the attention matrix. Conversely, implementing more dynamic sparse attentions often results in runtimes significantly slower than computing the full attention using the Flash implementation from Dao et al. (2022). We extend FlashAttention to accommodate a large class of attention sparsity patterns that, in particular, encompass key/query dropping and hashing-based attention. This leads to implementations with no computational complexity overhead and a multi-fold runtime speedup on top of FlashAttention. Even with relatively low degrees of sparsity, our method improves visibly upon FlashAttention as the sequence length increases. Without sacrificing perplexity, we increase the training speed of a transformer language model by $2.0\times$ and $3.3\times$ for sequences of respectively $8k$ and $16k$ tokens.

Revisiting the ACVI Method for Constrained Variational Inequalities

ACVI is a recently proposed first-order method for solving variational inequalities (VIs) with general constraints. Yang et al. (2022) showed that the gap function of the last iterate decreases at a rate of $\mathcal{O}(\frac{1}{\sqrt{K}})$ when the operator is $L$-Lipschitz, monotone, and at least one constraint is active. In this work, we show that the same guarantee holds when only assuming that the operator is monotone. To our knowledge, this is the first analytically derived last-iterate convergence rate for general monotone VIs, and overall the only one that does not rely on the assumption that the operator is $L$-Lipschitz. Furthermore, when the sub-problems of ACVI are solved approximately, we show that by using a standard warm-start technique the convergence rate stays the same, provided that the errors decrease at appropriate rates. We further provide empirical analyses and insights on its implementation for the latter case.

Improving Generalization via Uncertainty Driven Perturbations

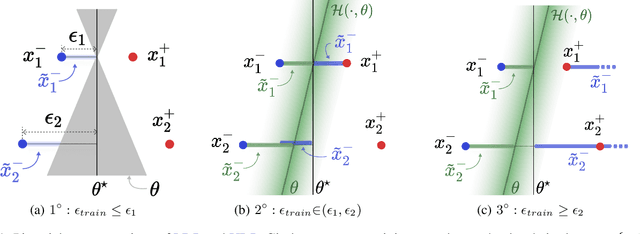
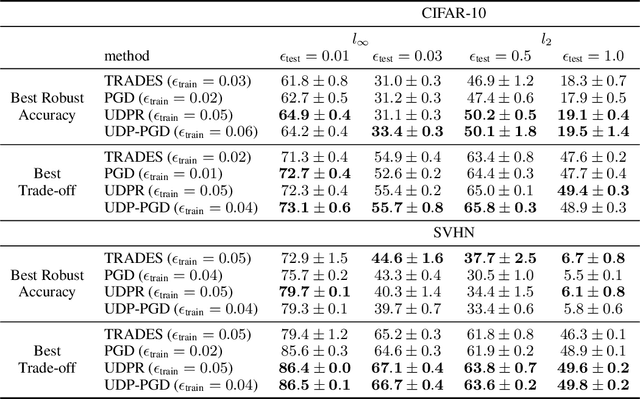
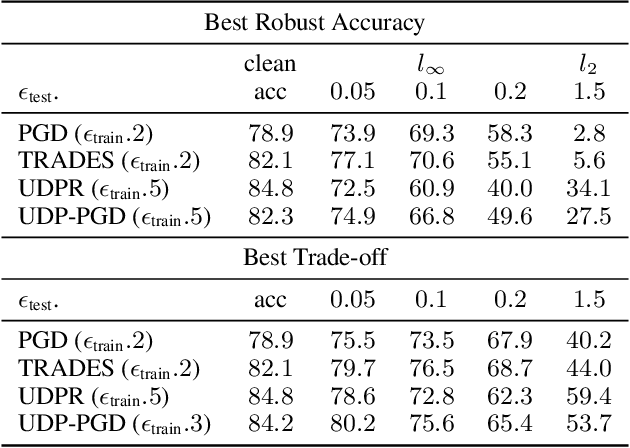
Recently Shah et al., 2020 pointed out the pitfalls of the simplicity bias - the tendency of gradient-based algorithms to learn simple models - which include the model's high sensitivity to small input perturbations, as well as sub-optimal margins. In particular, while Stochastic Gradient Descent yields max-margin boundary on linear models, such guarantee does not extend to non-linear models. To mitigate the simplicity bias, we consider uncertainty-driven perturbations (UDP) of the training data points, obtained iteratively by following the direction that maximizes the model's estimated uncertainty. The uncertainty estimate does not rely on the input's label and it is highest at the decision boundary, and - unlike loss-driven perturbations - it allows for using a larger range of values for the perturbation magnitude. Furthermore, as real-world datasets have non-isotropic distances between data points of different classes, the above property is particularly appealing for increasing the margin of the decision boundary, which in turn improves the model's generalization. We show that UDP is guaranteed to achieve the maximum margin decision boundary on linear models and that it notably increases it on challenging simulated datasets. For nonlinear models, we show empirically that UDP reduces the simplicity bias and learns more exhaustive features. Interestingly, it also achieves competitive loss-based robustness and generalization trade-off on several datasets.