Improving Generalization via Uncertainty Driven Perturbations
Paper and Code
Feb 28, 2022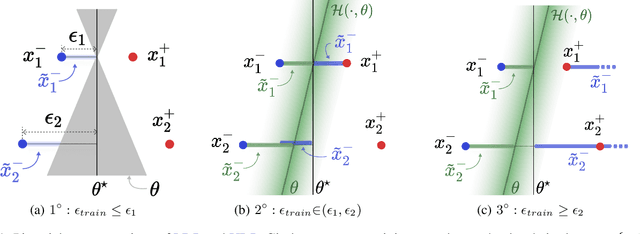
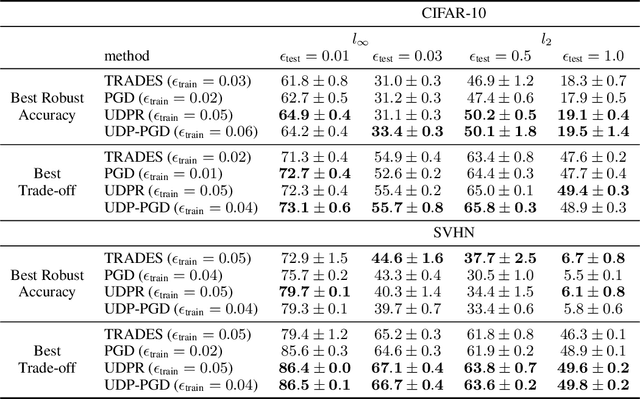
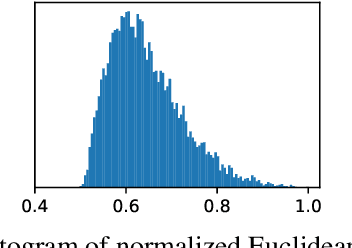
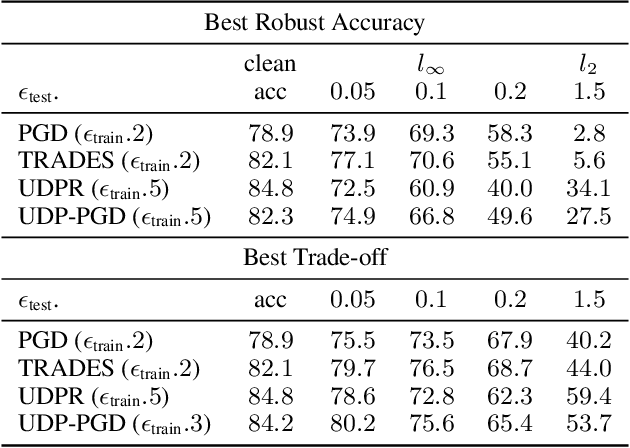
Recently Shah et al., 2020 pointed out the pitfalls of the simplicity bias - the tendency of gradient-based algorithms to learn simple models - which include the model's high sensitivity to small input perturbations, as well as sub-optimal margins. In particular, while Stochastic Gradient Descent yields max-margin boundary on linear models, such guarantee does not extend to non-linear models. To mitigate the simplicity bias, we consider uncertainty-driven perturbations (UDP) of the training data points, obtained iteratively by following the direction that maximizes the model's estimated uncertainty. The uncertainty estimate does not rely on the input's label and it is highest at the decision boundary, and - unlike loss-driven perturbations - it allows for using a larger range of values for the perturbation magnitude. Furthermore, as real-world datasets have non-isotropic distances between data points of different classes, the above property is particularly appealing for increasing the margin of the decision boundary, which in turn improves the model's generalization. We show that UDP is guaranteed to achieve the maximum margin decision boundary on linear models and that it notably increases it on challenging simulated datasets. For nonlinear models, we show empirically that UDP reduces the simplicity bias and learns more exhaustive features. Interestingly, it also achieves competitive loss-based robustness and generalization trade-off on several datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge