A New Class of Upper Bounds on the Log Partition Function

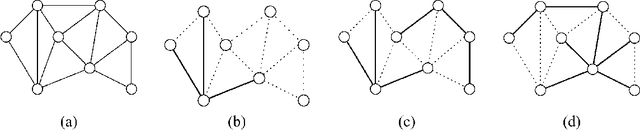
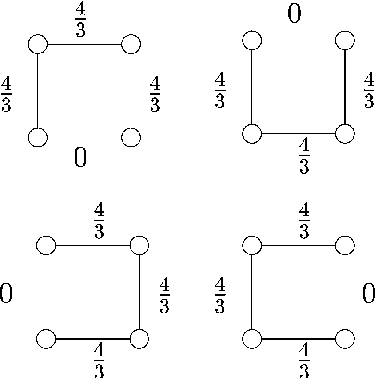
Bounds on the log partition function are important in a variety of contexts, including approximate inference, model fitting, decision theory, and large deviations analysis. We introduce a new class of upper bounds on the log partition function, based on convex combinations of distributions in the exponential domain, that is applicable to an arbitrary undirected graphical model. In the special case of convex combinations of tree-structured distributions, we obtain a family of variational problems, similar to the Bethe free energy, but distinguished by the following desirable properties: i. they are cnvex, and have a unique global minimum; and ii. the global minimum gives an upper bound on the log partition function. The global minimum is defined by stationary conditions very similar to those defining fixed points of belief propagation or tree-based reparameterization Wainwright et al., 2001. As with BP fixed points, the elements of the minimizing argument can be used as approximations to the marginals of the original model. The analysis described here can be extended to structures of higher treewidth e.g., hypertrees, thereby making connections with more advanced approximations e.g., Kikuchi and variants Yedidia et al., 2001; Minka, 2001.

The Hierarchical Dirichlet Process Hidden Semi-Markov Model

There is much interest in the Hierarchical Dirichlet Process Hidden Markov Model (HDP-HMM) as a natural Bayesian nonparametric extension of the traditional HMM. However, in many settings the HDP-HMM's strict Markovian constraints are undesirable, particularly if we wish to learn or encode non-geometric state durations. We can extend the HDP-HMM to capture such structure by drawing upon explicit-duration semi-Markovianity, which has been developed in the parametric setting to allow construction of highly interpretable models that admit natural prior information on state durations. In this paper we introduce the explicitduration HDP-HSMM and develop posterior sampling algorithms for efficient inference in both the direct-assignment and weak-limit approximation settings. We demonstrate the utility of the model and our inference methods on synthetic data as well as experiments on a speaker diarization problem and an example of learning the patterns in Morse code.

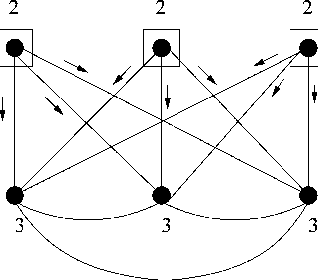
Message-passing for Maximum Weight Independent Set

We investigate the use of message-passing algorithms for the problem of finding the max-weight independent set (MWIS) in a graph. First, we study the performance of the classical loopy max-product belief propagation. We show that each fixed point estimate of max-product can be mapped in a natural way to an extreme point of the LP polytope associated with the MWIS problem. However, this extreme point may not be the one that maximizes the value of node weights; the particular extreme point at final convergence depends on the initialization of max-product. We then show that if max-product is started from the natural initialization of uninformative messages, it always solves the correct LP -- if it converges. This result is obtained via a direct analysis of the iterative algorithm, and cannot be obtained by looking only at fixed points. The tightness of the LP relaxation is thus necessary for max-product optimality, but it is not sufficient. Motivated by this observation, we show that a simple modification of max-product becomes gradient descent on (a convexified version of) the dual of the LP, and converges to the dual optimum. We also develop a message-passing algorithm that recovers the primal MWIS solution from the output of the descent algorithm. We show that the MWIS estimate obtained using these two algorithms in conjunction is correct when the graph is bipartite and the MWIS is unique. Finally, we show that any problem of MAP estimation for probability distributions over finite domains can be reduced to an MWIS problem. We believe this reduction will yield new insights and algorithms for MAP estimation.