Decomposing reverse-mode automatic differentiation

We decompose reverse-mode automatic differentiation into (forward-mode) linearization followed by transposition. Doing so isolates the essential difference between forward- and reverse-mode AD, and simplifies their joint implementation. In particular, once forward-mode AD rules are defined for every primitive operation in a source language, only linear primitives require an additional transposition rule in order to arrive at a complete reverse-mode AD implementation. This is how reverse-mode AD is written in JAX and Dex.

SOLAR: Deep Structured Representations for Model-Based Reinforcement Learning

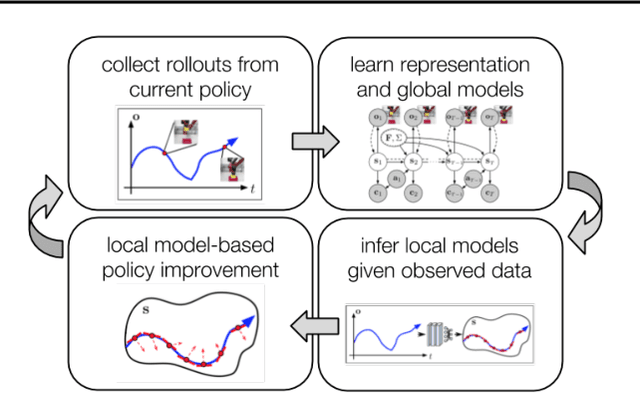
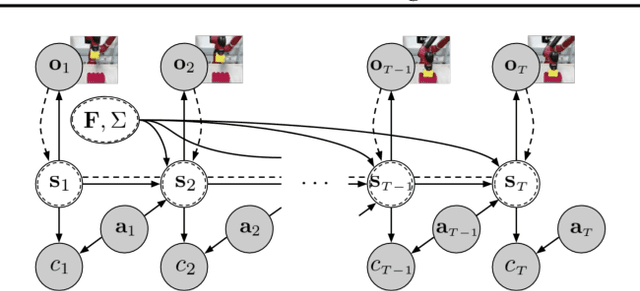
Model-based reinforcement learning (RL) has proven to be a data efficient approach for learning control tasks but is difficult to utilize in domains with complex observations such as images. In this paper, we present a method for learning representations that are suitable for iterative model-based policy improvement, in that these representations are optimized for inferring simple dynamics and cost models given data from the current policy. This enables a model-based RL method based on the linear-quadratic regulator (LQR) to be used for systems with image observations. We evaluate our approach on a suite of robotics tasks, including manipulation tasks on a real Sawyer robot arm directly from images, and we find that our method results in better final performance than other model-based RL methods while being significantly more efficient than model-free RL. Videos of our results are available at https://sites.google.com/view/icml19solar

Autoconj: Recognizing and Exploiting Conjugacy Without a Domain-Specific Language

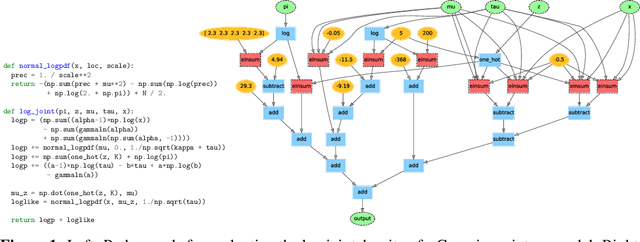
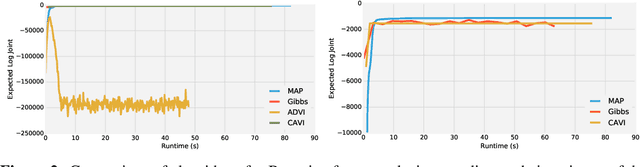
Deriving conditional and marginal distributions using conjugacy relationships can be time consuming and error prone. In this paper, we propose a strategy for automating such derivations. Unlike previous systems which focus on relationships between pairs of random variables, our system (which we call Autoconj) operates directly on Python functions that compute log-joint distribution functions. Autoconj provides support for conjugacy-exploiting algorithms in any Python embedded PPL. This paves the way for accelerating development of novel inference algorithms and structure-exploiting modeling strategies.

The LORACs prior for VAEs: Letting the Trees Speak for the Data

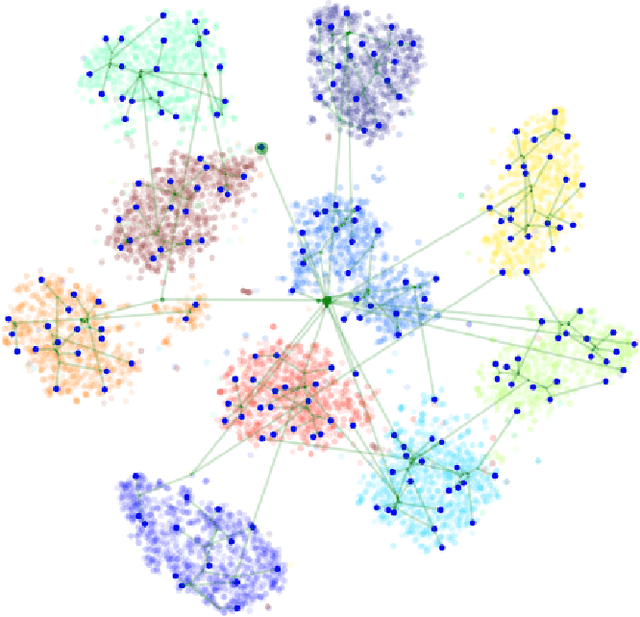
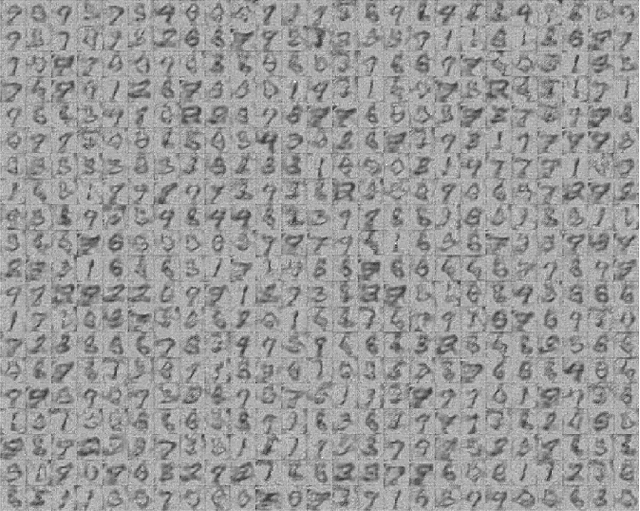
In variational autoencoders, the prior on the latent codes $z$ is often treated as an afterthought, but the prior shapes the kind of latent representation that the model learns. If the goal is to learn a representation that is interpretable and useful, then the prior should reflect the ways in which the high-level factors that describe the data vary. The "default" prior is an isotropic normal, but if the natural factors of variation in the dataset exhibit discrete structure or are not independent, then the isotropic-normal prior will actually encourage learning representations that mask this structure. To alleviate this problem, we propose using a flexible Bayesian nonparametric hierarchical clustering prior based on the time-marginalized coalescent (TMC). To scale learning to large datasets, we develop a new inducing-point approximation and inference algorithm. We then apply the method without supervision to several datasets and examine the interpretability and practical performance of the inferred hierarchies and learned latent space.

Estimating the Spectral Density of Large Implicit Matrices

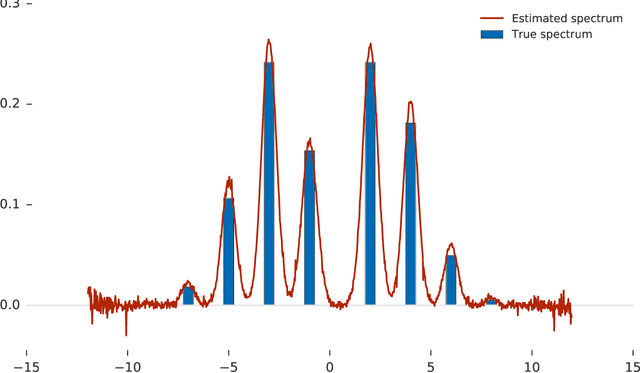
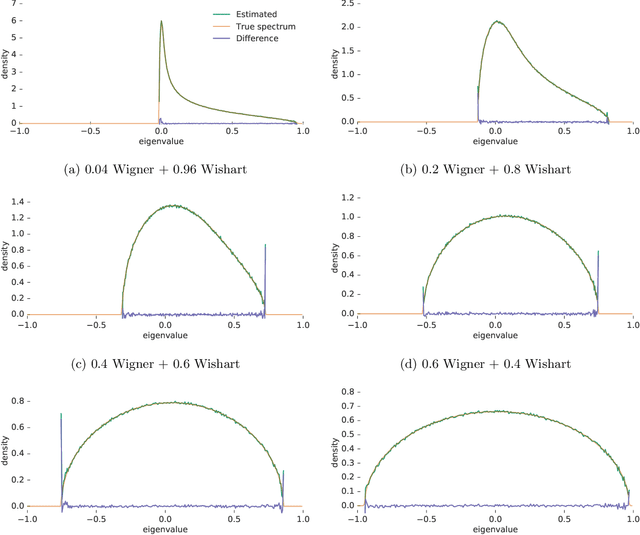
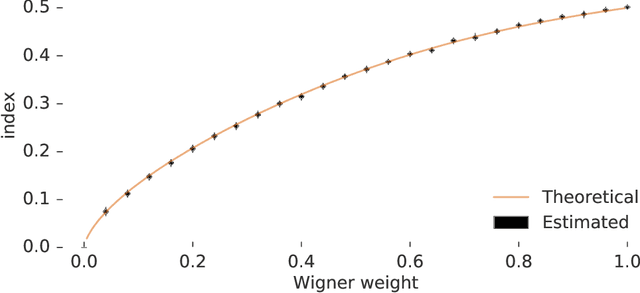
Many important problems are characterized by the eigenvalues of a large matrix. For example, the difficulty of many optimization problems, such as those arising from the fitting of large models in statistics and machine learning, can be investigated via the spectrum of the Hessian of the empirical loss function. Network data can be understood via the eigenstructure of a graph Laplacian matrix using spectral graph theory. Quantum simulations and other many-body problems are often characterized via the eigenvalues of the solution space, as are various dynamic systems. However, naive eigenvalue estimation is computationally expensive even when the matrix can be represented; in many of these situations the matrix is so large as to only be available implicitly via products with vectors. Even worse, one may only have noisy estimates of such matrix vector products. In this work, we combine several different techniques for randomized estimation and show that it is possible to construct unbiased estimators to answer a broad class of questions about the spectra of such implicit matrices, even in the presence of noise. We validate these methods on large-scale problems in which graph theory and random matrix theory provide ground truth.

Composing graphical models with neural networks for structured representations and fast inference

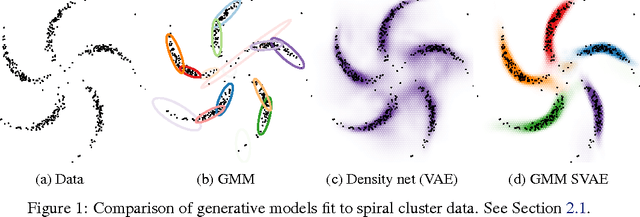
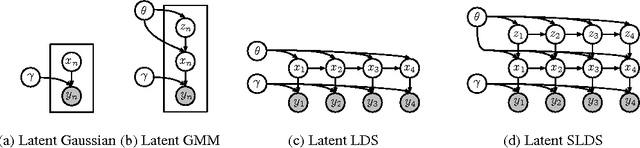
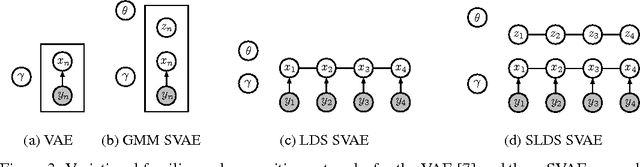
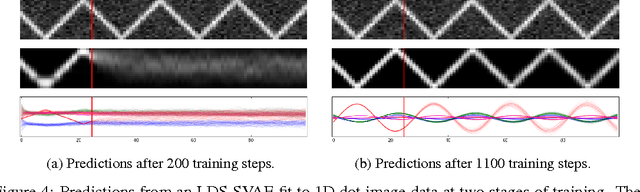
We propose a general modeling and inference framework that composes probabilistic graphical models with deep learning methods and combines their respective strengths. Our model family augments graphical structure in latent variables with neural network observation models. For inference, we extend variational autoencoders to use graphical model approximating distributions with recognition networks that output conjugate potentials. All components of these models are learned simultaneously with a single objective, giving a scalable algorithm that leverages stochastic variational inference, natural gradients, graphical model message passing, and the reparameterization trick. We illustrate this framework with several example models and an application to mouse behavioral phenotyping.

Multimodal Prediction and Personalization of Photo Edits with Deep Generative Models

Professional-grade software applications are powerful but complicated$-$expert users can achieve impressive results, but novices often struggle to complete even basic tasks. Photo editing is a prime example: after loading a photo, the user is confronted with an array of cryptic sliders like "clarity", "temp", and "highlights". An automatically generated suggestion could help, but there is no single "correct" edit for a given image$-$different experts may make very different aesthetic decisions when faced with the same image, and a single expert may make different choices depending on the intended use of the image (or on a whim). We therefore want a system that can propose multiple diverse, high-quality edits while also learning from and adapting to a user's aesthetic preferences. In this work, we develop a statistical model that meets these objectives. Our model builds on recent advances in neural network generative modeling and scalable inference, and uses hierarchical structure to learn editing patterns across many diverse users. Empirically, we find that our model outperforms other approaches on this challenging multimodal prediction task.

Recurrent switching linear dynamical systems

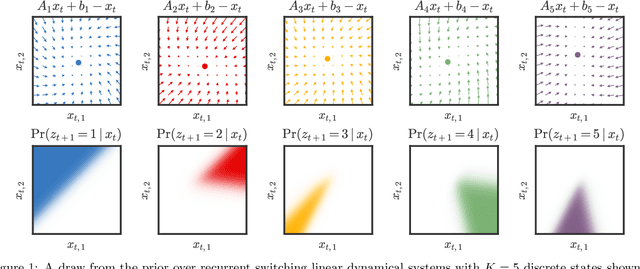
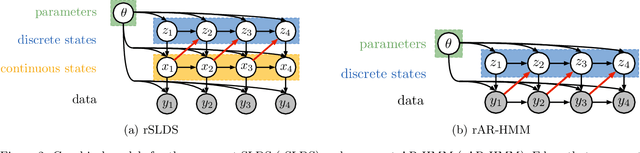
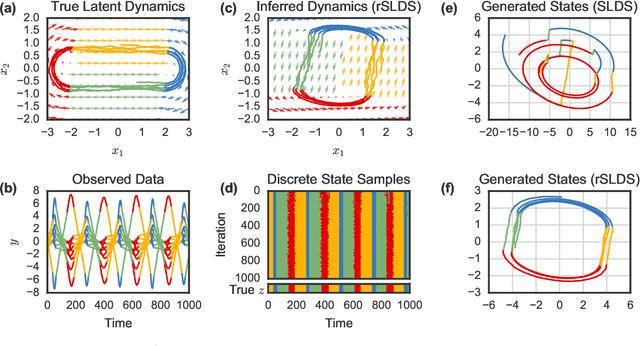
Many natural systems, such as neurons firing in the brain or basketball teams traversing a court, give rise to time series data with complex, nonlinear dynamics. We can gain insight into these systems by decomposing the data into segments that are each explained by simpler dynamic units. Building on switching linear dynamical systems (SLDS), we present a new model class that not only discovers these dynamical units, but also explains how their switching behavior depends on observations or continuous latent states. These "recurrent" switching linear dynamical systems provide further insight by discovering the conditions under which each unit is deployed, something that traditional SLDS models fail to do. We leverage recent algorithmic advances in approximate inference to make Bayesian inference in these models easy, fast, and scalable.

Dependent Multinomial Models Made Easy: Stick Breaking with the Pólya-Gamma Augmentation

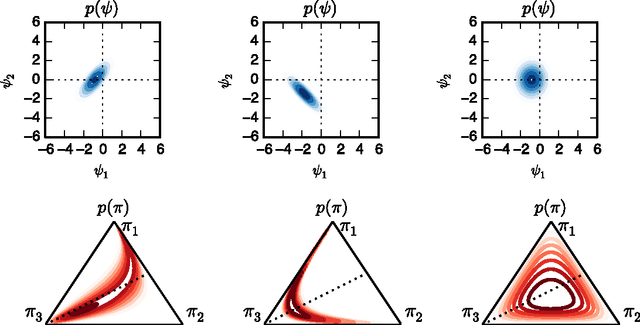
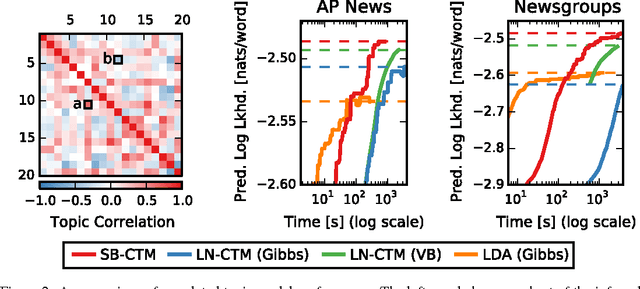
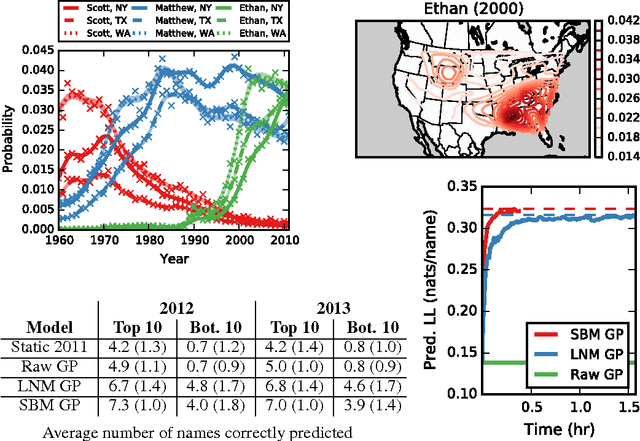
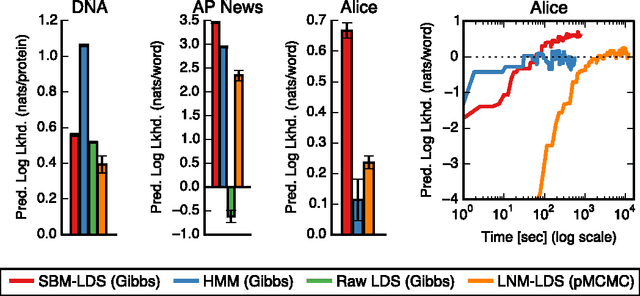
Many practical modeling problems involve discrete data that are best represented as draws from multinomial or categorical distributions. For example, nucleotides in a DNA sequence, children's names in a given state and year, and text documents are all commonly modeled with multinomial distributions. In all of these cases, we expect some form of dependency between the draws: the nucleotide at one position in the DNA strand may depend on the preceding nucleotides, children's names are highly correlated from year to year, and topics in text may be correlated and dynamic. These dependencies are not naturally captured by the typical Dirichlet-multinomial formulation. Here, we leverage a logistic stick-breaking representation and recent innovations in P\'olya-gamma augmentation to reformulate the multinomial distribution in terms of latent variables with jointly Gaussian likelihoods, enabling us to take advantage of a host of Bayesian inference techniques for Gaussian models with minimal overhead.

Detailed Derivations of Small-Variance Asymptotics for some Hierarchical Bayesian Nonparametric Models

In this note we provide detailed derivations of two versions of small-variance asymptotics for hierarchical Dirichlet process (HDP) mixture models and the HDP hidden Markov model (HDP-HMM, a.k.a. the infinite HMM). We include derivations for the probabilities of certain CRP and CRF partitions, which are of more general interest.