Robust Inverse Graphics via Probabilistic Inference

How do we infer a 3D scene from a single image in the presence of corruptions like rain, snow or fog? Straightforward domain randomization relies on knowing the family of corruptions ahead of time. Here, we propose a Bayesian approach-dubbed robust inverse graphics (RIG)-that relies on a strong scene prior and an uninformative uniform corruption prior, making it applicable to a wide range of corruptions. Given a single image, RIG performs posterior inference jointly over the scene and the corruption. We demonstrate this idea by training a neural radiance field (NeRF) scene prior and using a secondary NeRF to represent the corruptions over which we place an uninformative prior. RIG, trained only on clean data, outperforms depth estimators and alternative NeRF approaches that perform point estimation instead of full inference. The results hold for a number of scene prior architectures based on normalizing flows and diffusion models. For the latter, we develop reconstruction-guidance with auxiliary latents (ReGAL)-a diffusion conditioning algorithm that is applicable in the presence of auxiliary latent variables such as the corruption. RIG demonstrates how scene priors can be used beyond generation tasks.

Training Chain-of-Thought via Latent-Variable Inference

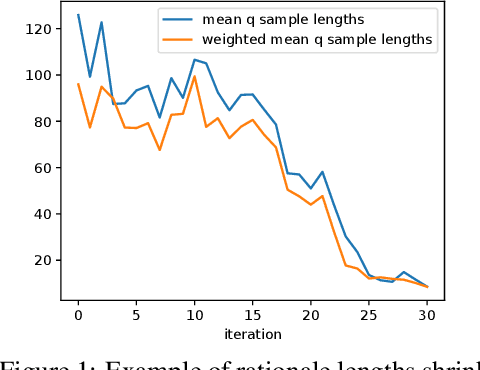
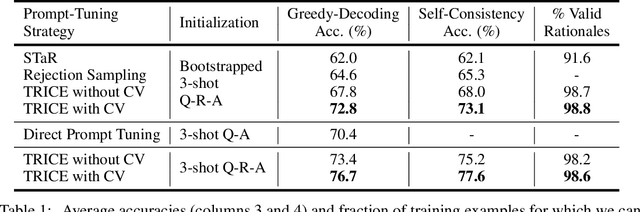
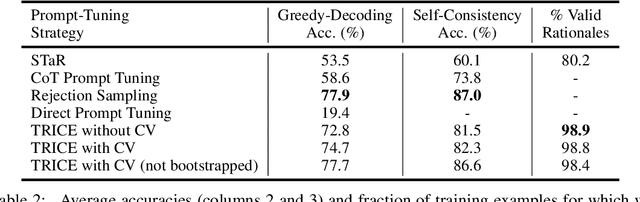
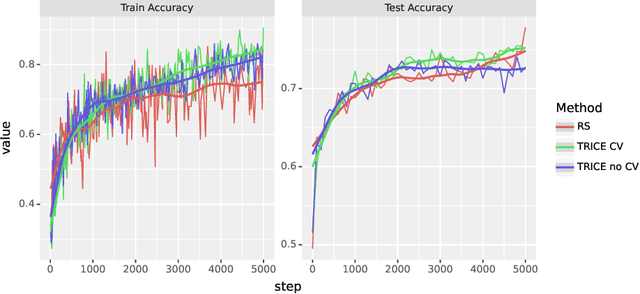
Large language models (LLMs) solve problems more accurately and interpretably when instructed to work out the answer step by step using a ``chain-of-thought'' (CoT) prompt. One can also improve LLMs' performance on a specific task by supervised fine-tuning, i.e., by using gradient ascent on some tunable parameters to maximize the average log-likelihood of correct answers from a labeled training set. Naively combining CoT with supervised tuning requires supervision not just of the correct answers, but also of detailed rationales that lead to those answers; these rationales are expensive to produce by hand. Instead, we propose a fine-tuning strategy that tries to maximize the \emph{marginal} log-likelihood of generating a correct answer using CoT prompting, approximately averaging over all possible rationales. The core challenge is sampling from the posterior over rationales conditioned on the correct answer; we address it using a simple Markov-chain Monte Carlo (MCMC) expectation-maximization (EM) algorithm inspired by the self-taught reasoner (STaR), memoized wake-sleep, Markovian score climbing, and persistent contrastive divergence. This algorithm also admits a novel control-variate technique that drives the variance of our gradient estimates to zero as the model improves. Applying our technique to GSM8K and the tasks in BIG-Bench Hard, we find that this MCMC-EM fine-tuning technique typically improves the model's accuracy on held-out examples more than STaR or prompt-tuning with or without CoT.

Sequential Monte Carlo Learning for Time Series Structure Discovery

This paper presents a new approach to automatically discovering accurate models of complex time series data. Working within a Bayesian nonparametric prior over a symbolic space of Gaussian process time series models, we present a novel structure learning algorithm that integrates sequential Monte Carlo (SMC) and involutive MCMC for highly effective posterior inference. Our method can be used both in "online" settings, where new data is incorporated sequentially in time, and in "offline" settings, by using nested subsets of historical data to anneal the posterior. Empirical measurements on real-world time series show that our method can deliver 10x--100x runtime speedups over previous MCMC and greedy-search structure learning algorithms targeting the same model family. We use our method to perform the first large-scale evaluation of Gaussian process time series structure learning on a prominent benchmark of 1,428 econometric datasets. The results show that our method discovers sensible models that deliver more accurate point forecasts and interval forecasts over multiple horizons as compared to widely used statistical and neural baselines that struggle on this challenging data.

ProbNeRF: Uncertainty-Aware Inference of 3D Shapes from 2D Images

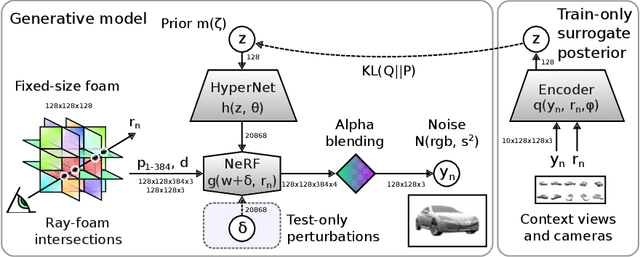
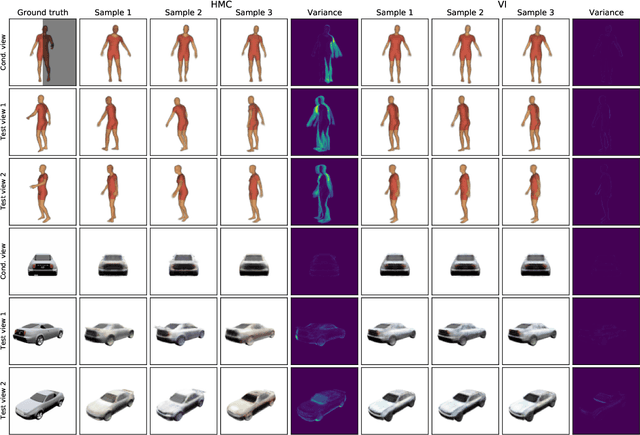
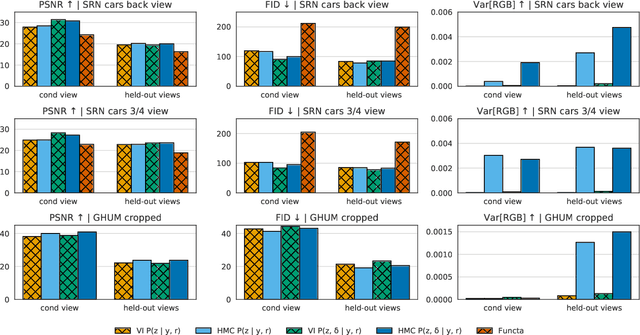
The problem of inferring object shape from a single 2D image is underconstrained. Prior knowledge about what objects are plausible can help, but even given such prior knowledge there may still be uncertainty about the shapes of occluded parts of objects. Recently, conditional neural radiance field (NeRF) models have been developed that can learn to infer good point estimates of 3D models from single 2D images. The problem of inferring uncertainty estimates for these models has received less attention. In this work, we propose probabilistic NeRF (ProbNeRF), a model and inference strategy for learning probabilistic generative models of 3D objects' shapes and appearances, and for doing posterior inference to recover those properties from 2D images. ProbNeRF is trained as a variational autoencoder, but at test time we use Hamiltonian Monte Carlo (HMC) for inference. Given one or a few 2D images of an object (which may be partially occluded), ProbNeRF is able not only to accurately model the parts it sees, but also to propose realistic and diverse hypotheses about the parts it does not see. We show that key to the success of ProbNeRF are (i) a deterministic rendering scheme, (ii) an annealed-HMC strategy, (iii) a hypernetwork-based decoder architecture, and (iv) doing inference over a full set of NeRF weights, rather than just a low-dimensional code.

Lossy Compression with Gaussian Diffusion

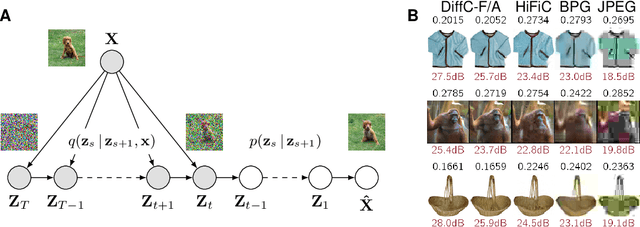
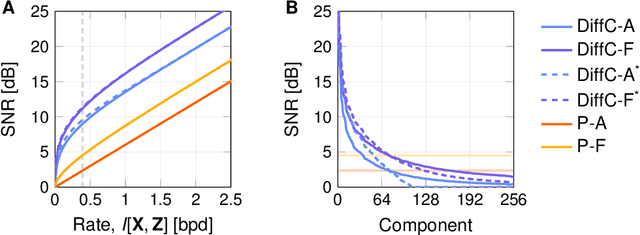
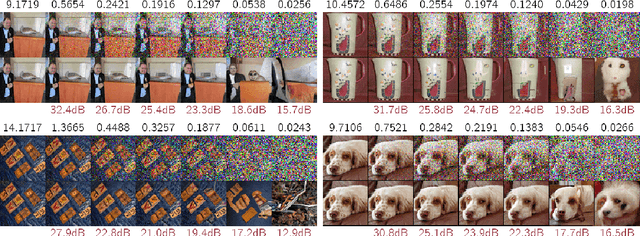
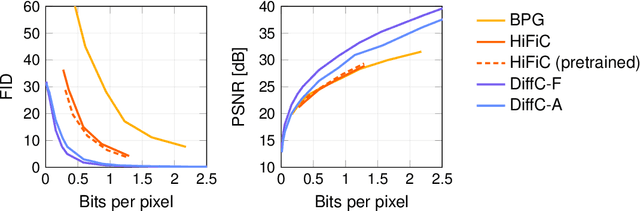
We describe a novel lossy compression approach called DiffC which is based on unconditional diffusion generative models. Unlike modern compression schemes which rely on transform coding and quantization to restrict the transmitted information, DiffC relies on the efficient communication of pixels corrupted by Gaussian noise. We implement a proof of concept and find that it works surprisingly well despite the lack of an encoder transform, outperforming the state-of-the-art generative compression method HiFiC on ImageNet 64x64. DiffC only uses a single model to encode and denoise corrupted pixels at arbitrary bitrates. The approach further provides support for progressive coding, that is, decoding from partial bit streams. We perform a rate-distortion analysis to gain a deeper understanding of its performance, providing analytical results for multivariate Gaussian data as well as initial results for general distributions. Furthermore, we show that a flow-based reconstruction achieves a 3 dB gain over ancestral sampling at high bitrates.

What Are Bayesian Neural Network Posteriors Really Like?

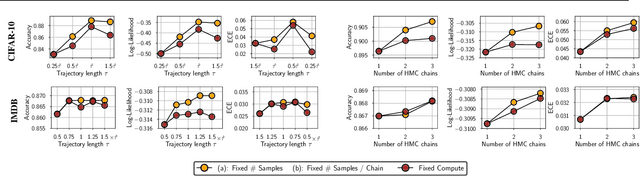
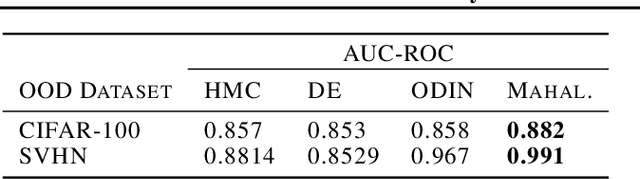
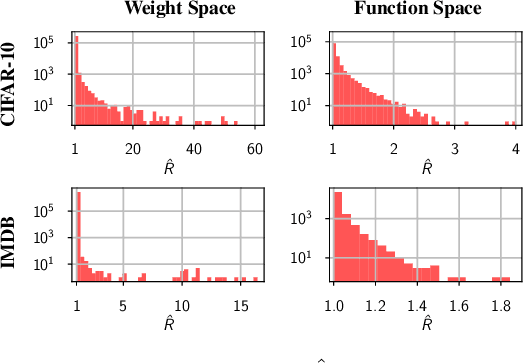
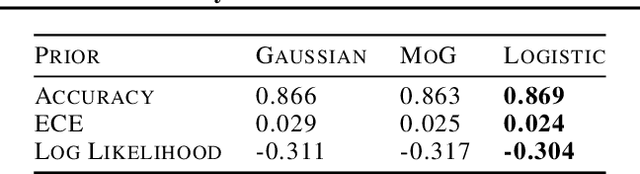
The posterior over Bayesian neural network (BNN) parameters is extremely high-dimensional and non-convex. For computational reasons, researchers approximate this posterior using inexpensive mini-batch methods such as mean-field variational inference or stochastic-gradient Markov chain Monte Carlo (SGMCMC). To investigate foundational questions in Bayesian deep learning, we instead use full-batch Hamiltonian Monte Carlo (HMC) on modern architectures. We show that (1) BNNs can achieve significant performance gains over standard training and deep ensembles; (2) a single long HMC chain can provide a comparable representation of the posterior to multiple shorter chains; (3) in contrast to recent studies, we find posterior tempering is not needed for near-optimal performance, with little evidence for a "cold posterior" effect, which we show is largely an artifact of data augmentation; (4) BMA performance is robust to the choice of prior scale, and relatively similar for diagonal Gaussian, mixture of Gaussian, and logistic priors; (5) Bayesian neural networks show surprisingly poor generalization under domain shift; (6) while cheaper alternatives such as deep ensembles and SGMCMC methods can provide good generalization, they provide distinct predictive distributions from HMC. Notably, deep ensemble predictive distributions are similarly close to HMC as standard SGLD, and closer than standard variational inference.

Underspecification Presents Challenges for Credibility in Modern Machine Learning

ML models often exhibit unexpectedly poor behavior when they are deployed in real-world domains. We identify underspecification as a key reason for these failures. An ML pipeline is underspecified when it can return many predictors with equivalently strong held-out performance in the training domain. Underspecification is common in modern ML pipelines, such as those based on deep learning. Predictors returned by underspecified pipelines are often treated as equivalent based on their training domain performance, but we show here that such predictors can behave very differently in deployment domains. This ambiguity can lead to instability and poor model behavior in practice, and is a distinct failure mode from previously identified issues arising from structural mismatch between training and deployment domains. We show that this problem appears in a wide variety of practical ML pipelines, using examples from computer vision, medical imaging, natural language processing, clinical risk prediction based on electronic health records, and medical genomics. Our results show the need to explicitly account for underspecification in modeling pipelines that are intended for real-world deployment in any domain.

tfp.mcmc: Modern Markov Chain Monte Carlo Tools Built for Modern Hardware

Markov chain Monte Carlo (MCMC) is widely regarded as one of the most important algorithms of the 20th century. Its guarantees of asymptotic convergence, stability, and estimator-variance bounds using only unnormalized probability functions make it indispensable to probabilistic programming. In this paper, we introduce the TensorFlow Probability MCMC toolkit, and discuss some of the considerations that motivated its design.

Automatically Batching Control-Intensive Programs for Modern Accelerators

We present a general approach to batching arbitrary computations for accelerators such as GPUs. We show orders-of-magnitude speedups using our method on the No U-Turn Sampler (NUTS), a workhorse algorithm in Bayesian statistics. The central challenge of batching NUTS and other Markov chain Monte Carlo algorithms is data-dependent control flow and recursion. We overcome this by mechanically transforming a single-example implementation into a form that explicitly tracks the current program point for each batch member, and only steps forward those in the same place. We present two different batching algorithms: a simpler, previously published one that inherits recursion from the host Python, and a more complex, novel one that implemenents recursion directly and can batch across it. We implement these batching methods as a general program transformation on Python source. Both the batching system and the NUTS implementation presented here are available as part of the popular TensorFlow Probability software package.

Automatic Reparameterisation of Probabilistic Programs

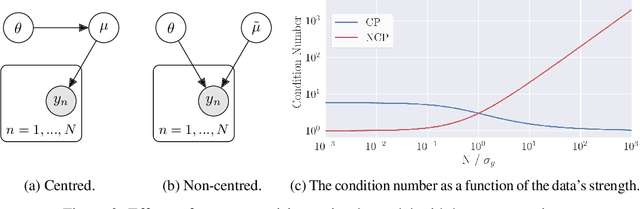
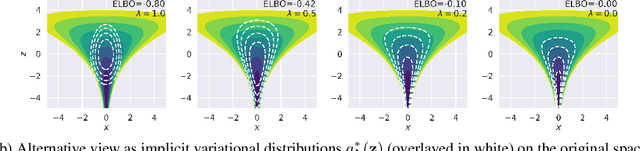
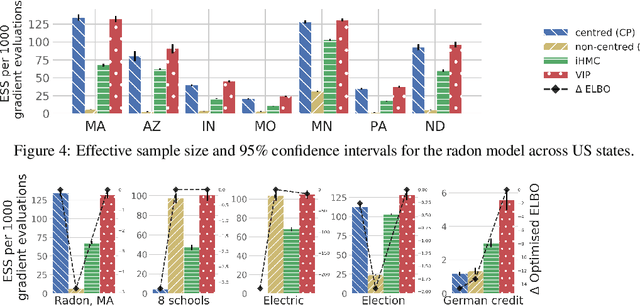
Probabilistic programming has emerged as a powerful paradigm in statistics, applied science, and machine learning: by decoupling modelling from inference, it promises to allow modellers to directly reason about the processes generating data. However, the performance of inference algorithms can be dramatically affected by the parameterisation used to express a model, requiring users to transform their programs in non-intuitive ways. We argue for automating these transformations, and demonstrate that mechanisms available in recent modeling frameworks can implement non-centring and related reparameterisations. This enables new inference algorithms, and we propose two: a simple approach using interleaved sampling and a novel variational formulation that searches over a continuous space of parameterisations. We show that these approaches enable robust inference across a range of models, and can yield more efficient samplers than the best fixed parameterisation.