ProbNeRF: Uncertainty-Aware Inference of 3D Shapes from 2D Images
Paper and Code
Oct 27, 2022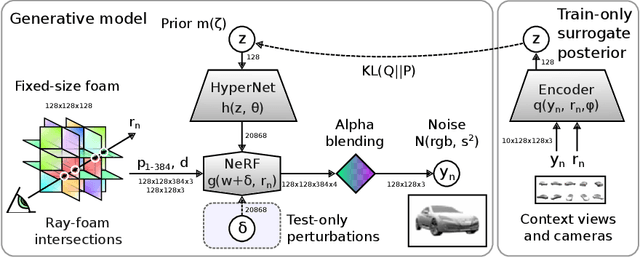

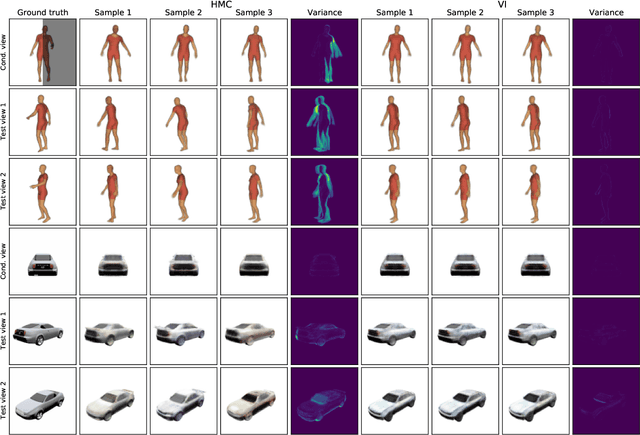
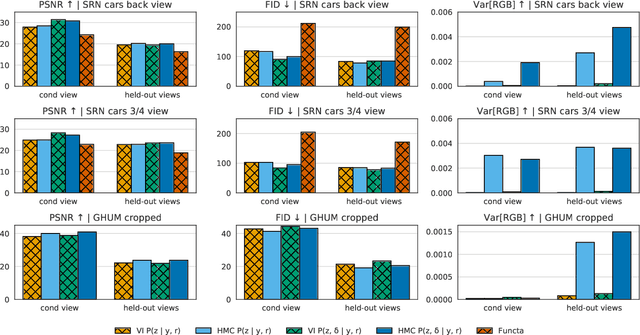
The problem of inferring object shape from a single 2D image is underconstrained. Prior knowledge about what objects are plausible can help, but even given such prior knowledge there may still be uncertainty about the shapes of occluded parts of objects. Recently, conditional neural radiance field (NeRF) models have been developed that can learn to infer good point estimates of 3D models from single 2D images. The problem of inferring uncertainty estimates for these models has received less attention. In this work, we propose probabilistic NeRF (ProbNeRF), a model and inference strategy for learning probabilistic generative models of 3D objects' shapes and appearances, and for doing posterior inference to recover those properties from 2D images. ProbNeRF is trained as a variational autoencoder, but at test time we use Hamiltonian Monte Carlo (HMC) for inference. Given one or a few 2D images of an object (which may be partially occluded), ProbNeRF is able not only to accurately model the parts it sees, but also to propose realistic and diverse hypotheses about the parts it does not see. We show that key to the success of ProbNeRF are (i) a deterministic rendering scheme, (ii) an annealed-HMC strategy, (iii) a hypernetwork-based decoder architecture, and (iv) doing inference over a full set of NeRF weights, rather than just a low-dimensional code.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge