Sequential Monte Carlo Learning for Time Series Structure Discovery

This paper presents a new approach to automatically discovering accurate models of complex time series data. Working within a Bayesian nonparametric prior over a symbolic space of Gaussian process time series models, we present a novel structure learning algorithm that integrates sequential Monte Carlo (SMC) and involutive MCMC for highly effective posterior inference. Our method can be used both in "online" settings, where new data is incorporated sequentially in time, and in "offline" settings, by using nested subsets of historical data to anneal the posterior. Empirical measurements on real-world time series show that our method can deliver 10x--100x runtime speedups over previous MCMC and greedy-search structure learning algorithms targeting the same model family. We use our method to perform the first large-scale evaluation of Gaussian process time series structure learning on a prominent benchmark of 1,428 econometric datasets. The results show that our method discovers sensible models that deliver more accurate point forecasts and interval forecasts over multiple horizons as compared to widely used statistical and neural baselines that struggle on this challenging data.

Estimators of Entropy and Information via Inference in Probabilistic Models

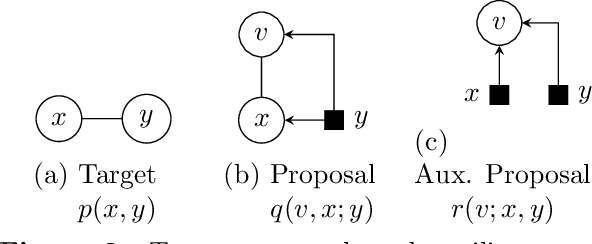
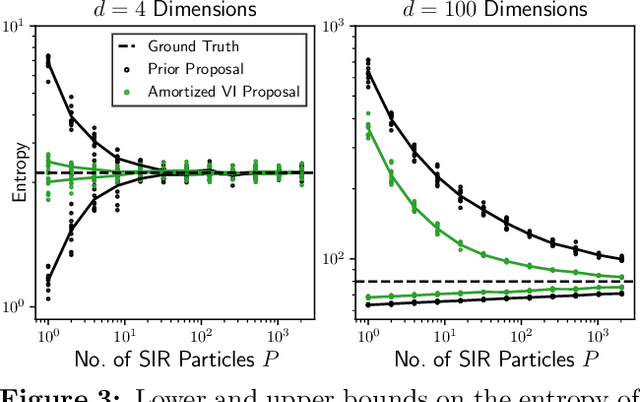
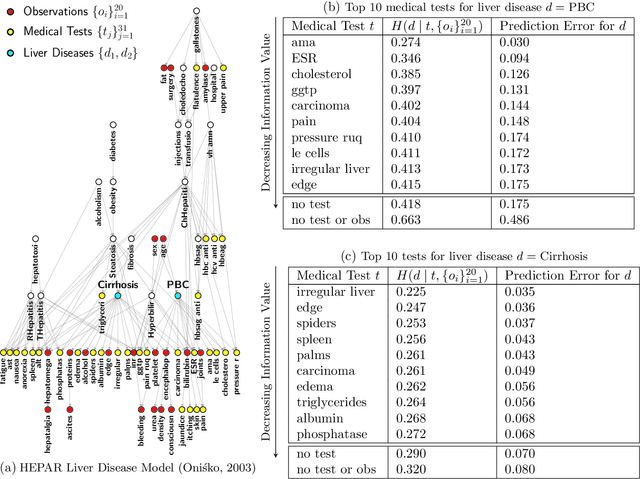
Estimating information-theoretic quantities such as entropy and mutual information is central to many problems in statistics and machine learning, but challenging in high dimensions. This paper presents estimators of entropy via inference (EEVI), which deliver upper and lower bounds on many information quantities for arbitrary variables in a probabilistic generative model. These estimators use importance sampling with proposal distribution families that include amortized variational inference and sequential Monte Carlo, which can be tailored to the target model and used to squeeze true information values with high accuracy. We present several theoretical properties of EEVI and demonstrate scalability and efficacy on two problems from the medical domain: (i) in an expert system for diagnosing liver disorders, we rank medical tests according to how informative they are about latent diseases, given a pattern of observed symptoms and patient attributes; and (ii) in a differential equation model of carbohydrate metabolism, we find optimal times to take blood glucose measurements that maximize information about a diabetic patient's insulin sensitivity, given their meal and medication schedule.

Hierarchical Infinite Relational Model

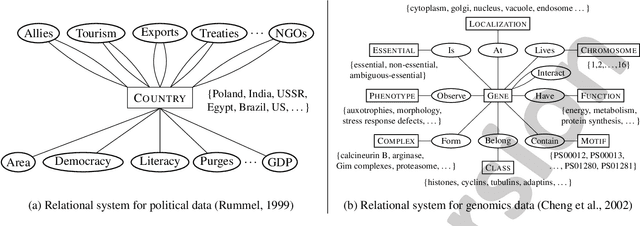
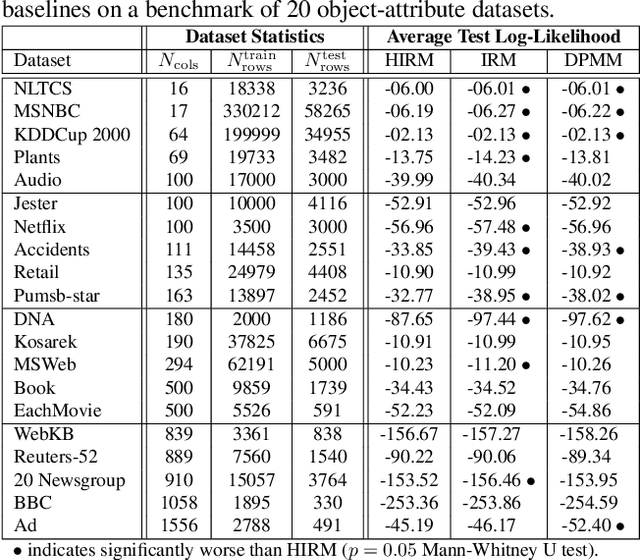
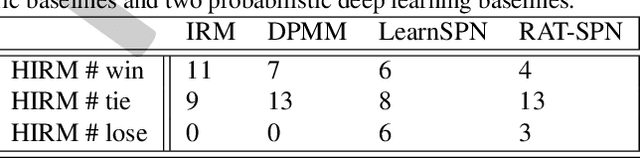
This paper describes the hierarchical infinite relational model (HIRM), a new probabilistic generative model for noisy, sparse, and heterogeneous relational data. Given a set of relations defined over a collection of domains, the model first infers multiple non-overlapping clusters of relations using a top-level Chinese restaurant process. Within each cluster of relations, a Dirichlet process mixture is then used to partition the domain entities and model the probability distribution of relation values. The HIRM generalizes the standard infinite relational model and can be used for a variety of data analysis tasks including dependence detection, clustering, and density estimation. We present new algorithms for fully Bayesian posterior inference via Gibbs sampling. We illustrate the efficacy of the method on a density estimation benchmark of twenty object-attribute datasets with up to 18 million cells and use it to discover relational structure in real-world datasets from politics and genomics.

Exact Symbolic Inference in Probabilistic Programs via Sum-Product Representations

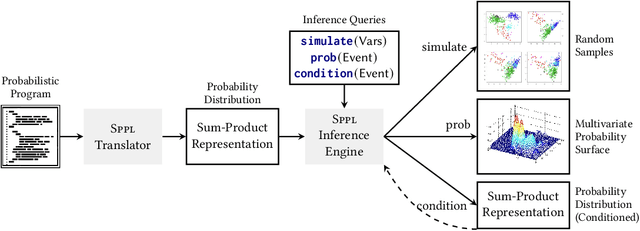
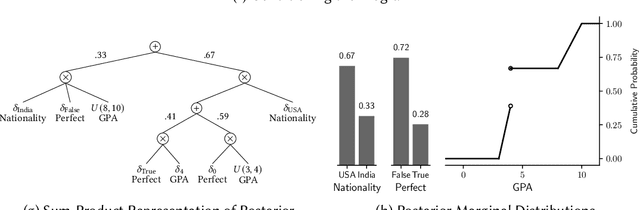
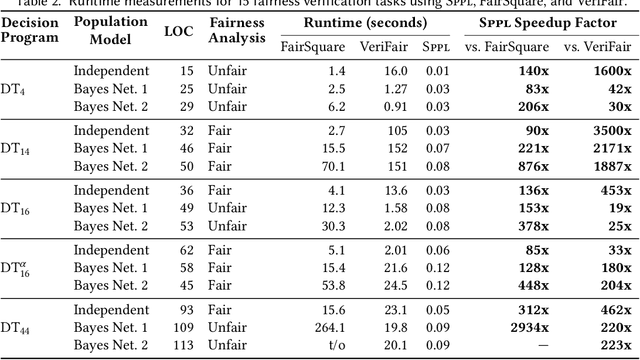
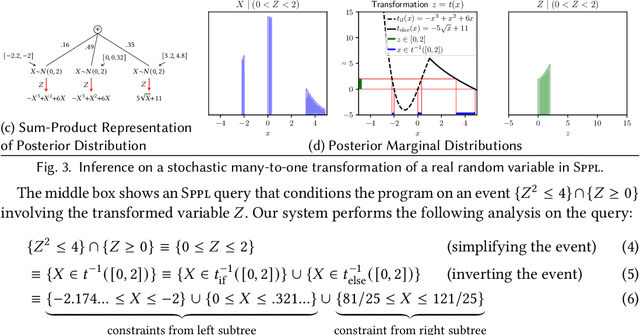
We present the Sum-Product Probabilistic Language (SPPL), a new system that automatically delivers exact solutions to a broad range of probabilistic inference queries. SPPL symbolically represents the full distribution on execution traces specified by a probabilistic program using a generalization of sum-product networks. SPPL handles continuous and discrete distributions, many-to-one numerical transformations, and a query language that includes general predicates on random variables. We formalize SPPL in terms of a novel translation strategy from probabilistic programs to a semantic domain of sum-product representations, present new algorithms for exactly conditioning on and computing probabilities of queries, and prove their soundness under the semantics. We present techniques for improving the scalability of translation and inference by automatically exploiting conditional independences and repeated structure in SPPL programs. We implement a prototype of SPPL with a modular architecture and evaluate it on a suite of common benchmarks, which establish that our system is up to 3500x faster than state-of-the-art systems for fairness verification; up to 1000x faster than state-of-the-art symbolic algebra techniques; and can compute exact probabilities of rare events in milliseconds.

Bayesian Synthesis of Probabilistic Programs for Automatic Data Modeling

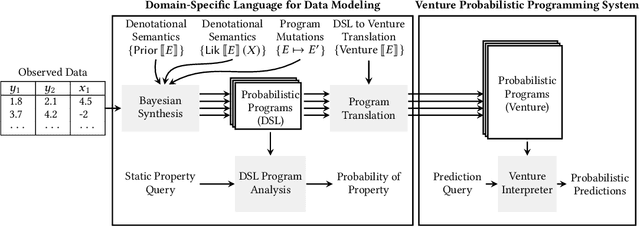
We present new techniques for automatically constructing probabilistic programs for data analysis, interpretation, and prediction. These techniques work with probabilistic domain-specific data modeling languages that capture key properties of a broad class of data generating processes, using Bayesian inference to synthesize probabilistic programs in these modeling languages given observed data. We provide a precise formulation of Bayesian synthesis for automatic data modeling that identifies sufficient conditions for the resulting synthesis procedure to be sound. We also derive a general class of synthesis algorithms for domain-specific languages specified by probabilistic context-free grammars and establish the soundness of our approach for these languages. We apply the techniques to automatically synthesize probabilistic programs for time series data and multivariate tabular data. We show how to analyze the structure of the synthesized programs to compute, for key qualitative properties of interest, the probability that the underlying data generating process exhibits each of these properties. Second, we translate probabilistic programs in the domain-specific language into probabilistic programs in Venture, a general-purpose probabilistic programming system. The translated Venture programs are then executed to obtain predictions of new time series data and new multivariate data records. Experimental results show that our techniques can accurately infer qualitative structure in multiple real-world data sets and outperform standard data analysis methods in forecasting and predicting new data.

A Family of Exact Goodness-of-Fit Tests for High-Dimensional Discrete Distributions

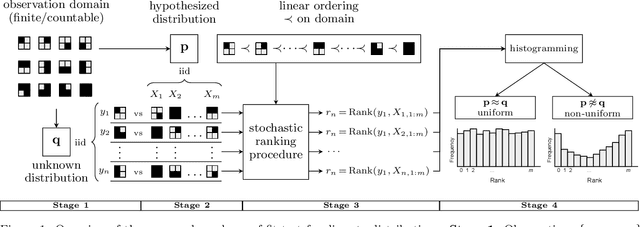
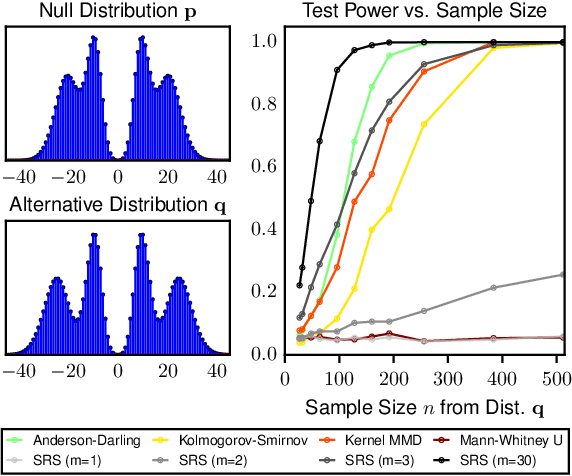
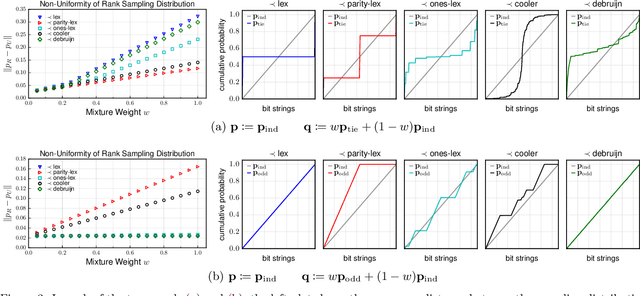
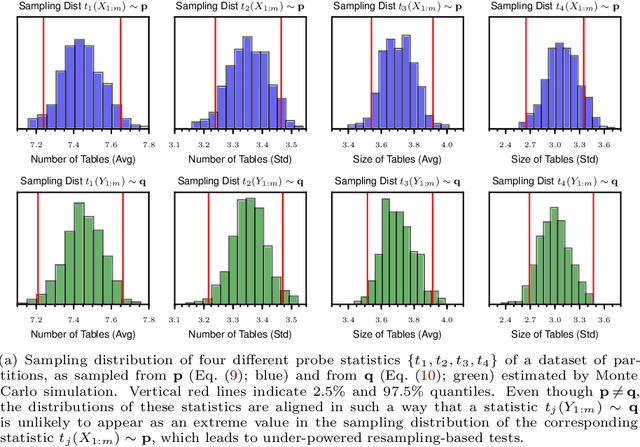
The objective of goodness-of-fit testing is to assess whether a dataset of observations is likely to have been drawn from a candidate probability distribution. This paper presents a rank-based family of goodness-of-fit tests that is specialized to discrete distributions on high-dimensional domains. The test is readily implemented using a simulation-based, linear-time procedure. The testing procedure can be customized by the practitioner using knowledge of the underlying data domain. Unlike most existing test statistics, the proposed test statistic is distribution-free and its exact (non-asymptotic) sampling distribution is known in closed form. We establish consistency of the test against all alternatives by showing that the test statistic is distributed as a discrete uniform if and only if the samples were drawn from the candidate distribution. We illustrate its efficacy for assessing the sample quality of approximate sampling algorithms over combinatorially large spaces with intractable probabilities, including random partitions in Dirichlet process mixture models and random lattices in Ising models.

Temporally-Reweighted Chinese Restaurant Process Mixtures for Clustering, Imputing, and Forecasting Multivariate Time Series

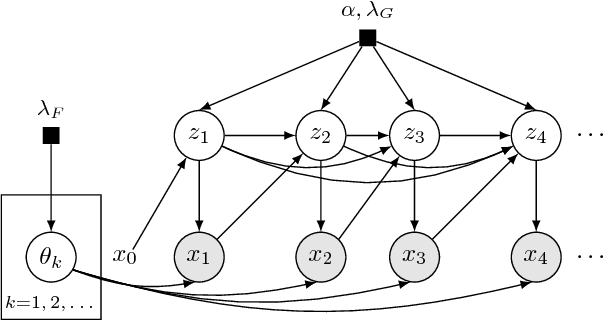
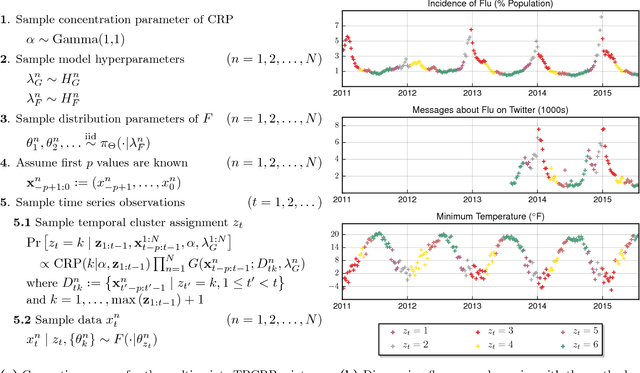
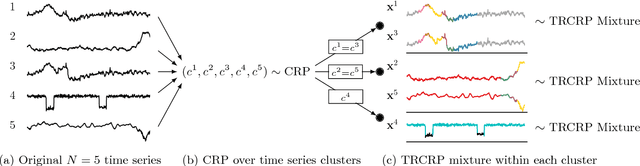
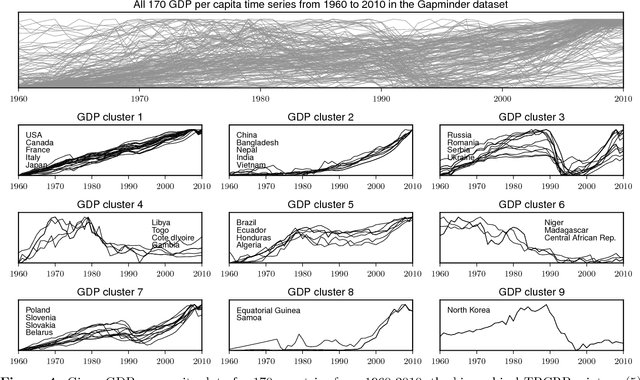
This article proposes a Bayesian nonparametric method for forecasting, imputation, and clustering in sparsely observed, multivariate time series data. The method is appropriate for jointly modeling hundreds of time series with widely varying, non-stationary dynamics. Given a collection of $N$ time series, the Bayesian model first partitions them into independent clusters using a Chinese restaurant process prior. Within a cluster, all time series are modeled jointly using a novel "temporally-reweighted" extension of the Chinese restaurant process mixture. Markov chain Monte Carlo techniques are used to obtain samples from the posterior distribution, which are then used to form predictive inferences. We apply the technique to challenging forecasting and imputation tasks using seasonal flu data from the US Center for Disease Control and Prevention, demonstrating superior forecasting accuracy and competitive imputation accuracy as compared to multiple widely used baselines. We further show that the model discovers interpretable clusters in datasets with hundreds of time series, using macroeconomic data from the Gapminder Foundation.