A Family of Exact Goodness-of-Fit Tests for High-Dimensional Discrete Distributions

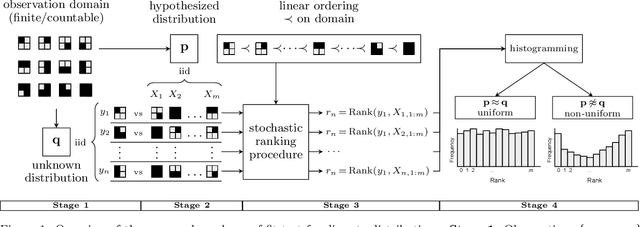
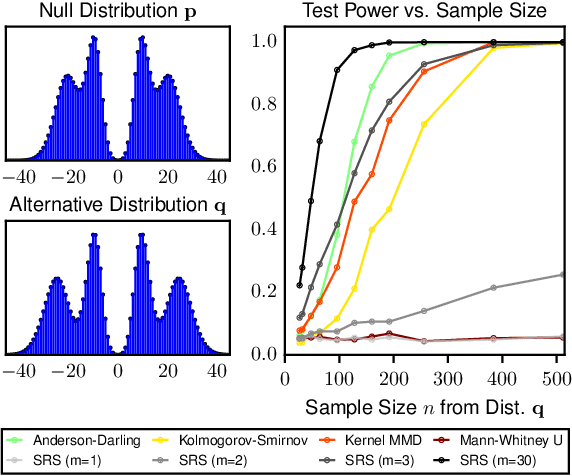
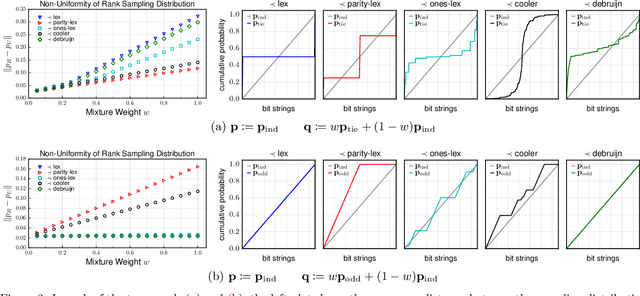
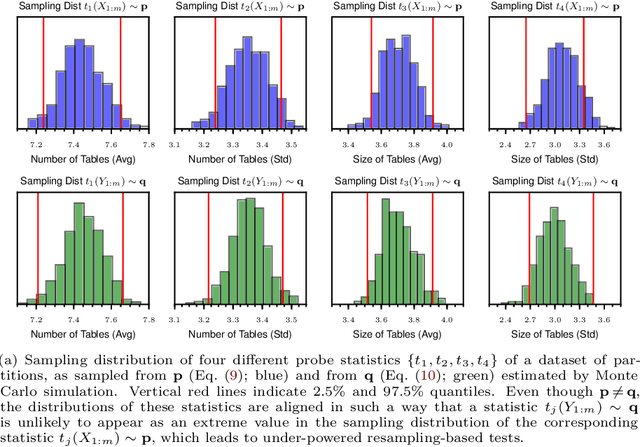
The objective of goodness-of-fit testing is to assess whether a dataset of observations is likely to have been drawn from a candidate probability distribution. This paper presents a rank-based family of goodness-of-fit tests that is specialized to discrete distributions on high-dimensional domains. The test is readily implemented using a simulation-based, linear-time procedure. The testing procedure can be customized by the practitioner using knowledge of the underlying data domain. Unlike most existing test statistics, the proposed test statistic is distribution-free and its exact (non-asymptotic) sampling distribution is known in closed form. We establish consistency of the test against all alternatives by showing that the test statistic is distributed as a discrete uniform if and only if the samples were drawn from the candidate distribution. We illustrate its efficacy for assessing the sample quality of approximate sampling algorithms over combinatorially large spaces with intractable probabilities, including random partitions in Dirichlet process mixture models and random lattices in Ising models.

On the computability of conditional probability

As inductive inference and machine learning methods in computer science see continued success, researchers are aiming to describe even more complex probabilistic models and inference algorithms. What are the limits of mechanizing probabilistic inference? We investigate the computability of conditional probability, a fundamental notion in probability theory and a cornerstone of Bayesian statistics, and show that there are computable joint distributions with noncomputable conditional distributions, ruling out the prospect of general inference algorithms, even inefficient ones. Specifically, we construct a pair of computable random variables in the unit interval such that the conditional distribution of the first variable given the second encodes the halting problem. Nevertheless, probabilistic inference is possible in many common modeling settings, and we prove several results giving broadly applicable conditions under which conditional distributions are computable. In particular, conditional distributions become computable when measurements are corrupted by independent computable noise with a sufficiently smooth density.