Probabilistic Programming with Programmable Variational Inference

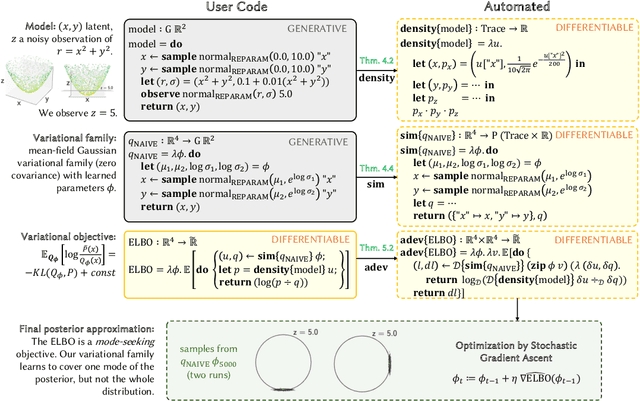
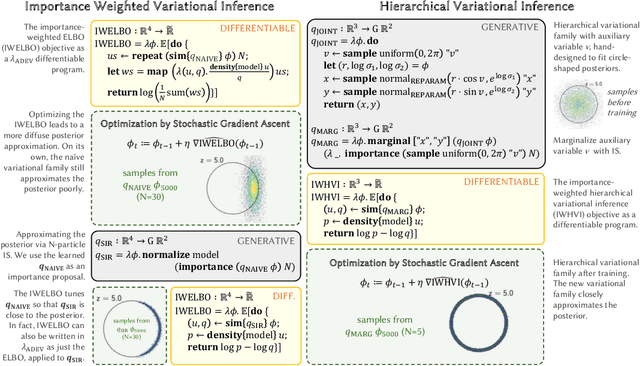
Compared to the wide array of advanced Monte Carlo methods supported by modern probabilistic programming languages (PPLs), PPL support for variational inference (VI) is less developed: users are typically limited to a predefined selection of variational objectives and gradient estimators, which are implemented monolithically (and without formal correctness arguments) in PPL backends. In this paper, we propose a more modular approach to supporting variational inference in PPLs, based on compositional program transformation. In our approach, variational objectives are expressed as programs, that may employ first-class constructs for computing densities of and expected values under user-defined models and variational families. We then transform these programs systematically into unbiased gradient estimators for optimizing the objectives they define. Our design enables modular reasoning about many interacting concerns, including automatic differentiation, density accumulation, tracing, and the application of unbiased gradient estimation strategies. Additionally, relative to existing support for VI in PPLs, our design increases expressiveness along three axes: (1) it supports an open-ended set of user-defined variational objectives, rather than a fixed menu of options; (2) it supports a combinatorial space of gradient estimation strategies, many not automated by today's PPLs; and (3) it supports a broader class of models and variational families, because it supports constructs for approximate marginalization and normalization (previously introduced only for Monte Carlo inference). We implement our approach in an extension to the Gen probabilistic programming system (genjax.vi, implemented in JAX), and evaluate on several deep generative modeling tasks, showing minimal performance overhead vs. hand-coded implementations and performance competitive with well-established open-source PPLs.

Exact Symbolic Inference in Probabilistic Programs via Sum-Product Representations

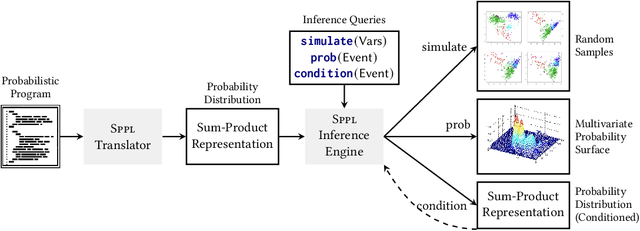
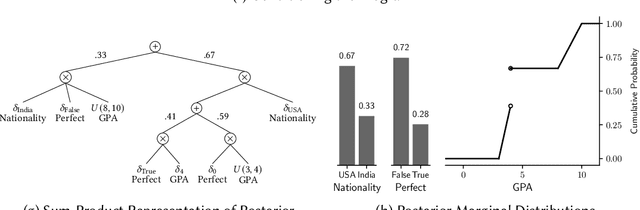
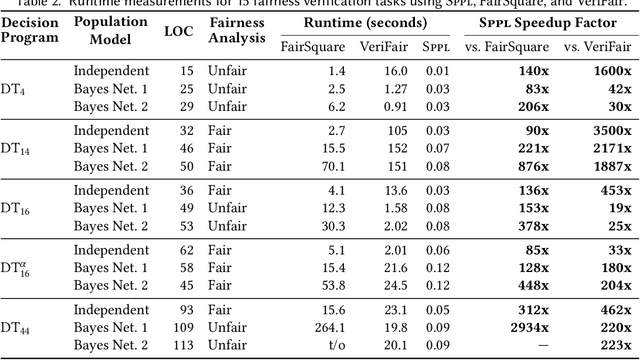
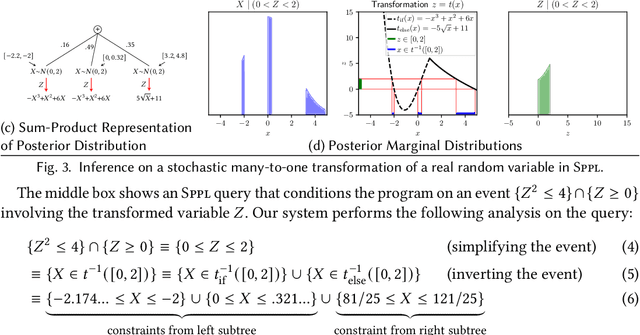
We present the Sum-Product Probabilistic Language (SPPL), a new system that automatically delivers exact solutions to a broad range of probabilistic inference queries. SPPL symbolically represents the full distribution on execution traces specified by a probabilistic program using a generalization of sum-product networks. SPPL handles continuous and discrete distributions, many-to-one numerical transformations, and a query language that includes general predicates on random variables. We formalize SPPL in terms of a novel translation strategy from probabilistic programs to a semantic domain of sum-product representations, present new algorithms for exactly conditioning on and computing probabilities of queries, and prove their soundness under the semantics. We present techniques for improving the scalability of translation and inference by automatically exploiting conditional independences and repeated structure in SPPL programs. We implement a prototype of SPPL with a modular architecture and evaluate it on a suite of common benchmarks, which establish that our system is up to 3500x faster than state-of-the-art systems for fairness verification; up to 1000x faster than state-of-the-art symbolic algebra techniques; and can compute exact probabilities of rare events in milliseconds.

Bayesian Synthesis of Probabilistic Programs for Automatic Data Modeling

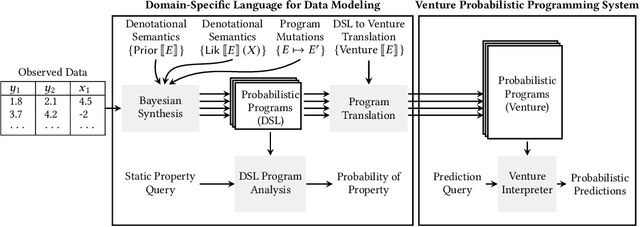
We present new techniques for automatically constructing probabilistic programs for data analysis, interpretation, and prediction. These techniques work with probabilistic domain-specific data modeling languages that capture key properties of a broad class of data generating processes, using Bayesian inference to synthesize probabilistic programs in these modeling languages given observed data. We provide a precise formulation of Bayesian synthesis for automatic data modeling that identifies sufficient conditions for the resulting synthesis procedure to be sound. We also derive a general class of synthesis algorithms for domain-specific languages specified by probabilistic context-free grammars and establish the soundness of our approach for these languages. We apply the techniques to automatically synthesize probabilistic programs for time series data and multivariate tabular data. We show how to analyze the structure of the synthesized programs to compute, for key qualitative properties of interest, the probability that the underlying data generating process exhibits each of these properties. Second, we translate probabilistic programs in the domain-specific language into probabilistic programs in Venture, a general-purpose probabilistic programming system. The translated Venture programs are then executed to obtain predictions of new time series data and new multivariate data records. Experimental results show that our techniques can accurately infer qualitative structure in multiple real-world data sets and outperform standard data analysis methods in forecasting and predicting new data.