Exact Symbolic Inference in Probabilistic Programs via Sum-Product Representations

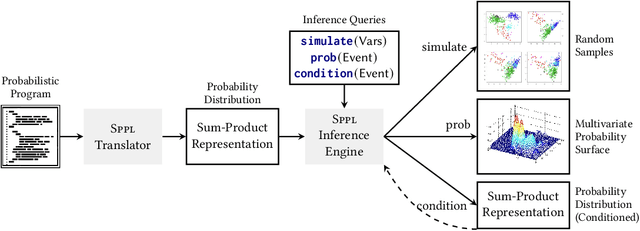
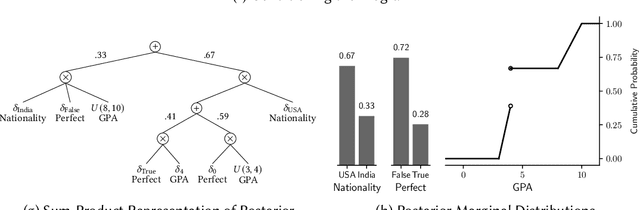
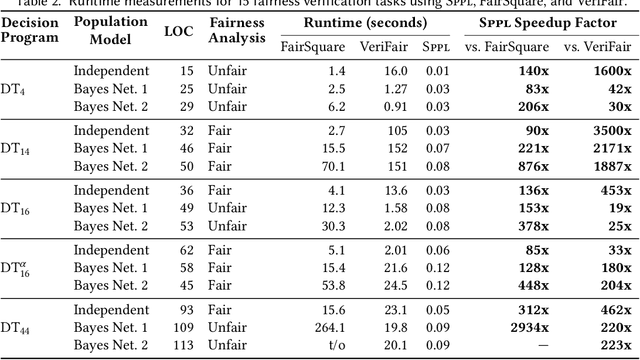
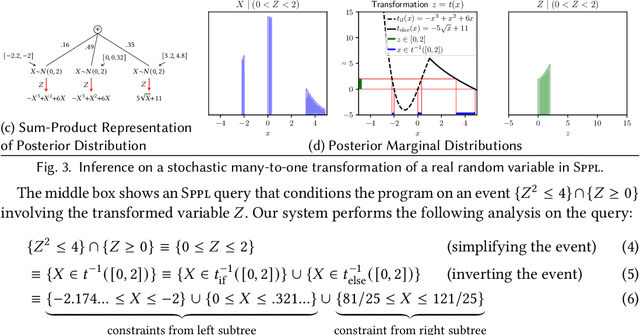
We present the Sum-Product Probabilistic Language (SPPL), a new system that automatically delivers exact solutions to a broad range of probabilistic inference queries. SPPL symbolically represents the full distribution on execution traces specified by a probabilistic program using a generalization of sum-product networks. SPPL handles continuous and discrete distributions, many-to-one numerical transformations, and a query language that includes general predicates on random variables. We formalize SPPL in terms of a novel translation strategy from probabilistic programs to a semantic domain of sum-product representations, present new algorithms for exactly conditioning on and computing probabilities of queries, and prove their soundness under the semantics. We present techniques for improving the scalability of translation and inference by automatically exploiting conditional independences and repeated structure in SPPL programs. We implement a prototype of SPPL with a modular architecture and evaluate it on a suite of common benchmarks, which establish that our system is up to 3500x faster than state-of-the-art systems for fairness verification; up to 1000x faster than state-of-the-art symbolic algebra techniques; and can compute exact probabilities of rare events in milliseconds.