Ulrich Schaechtle
Bayesian Synthesis of Probabilistic Programs for Automatic Data Modeling
Jul 14, 2019
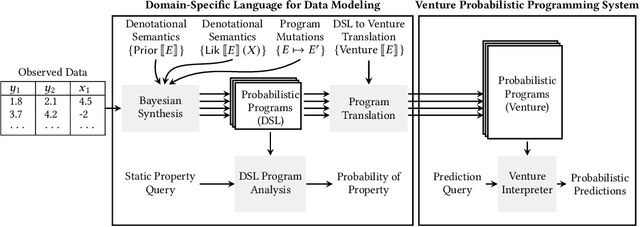


Abstract:We present new techniques for automatically constructing probabilistic programs for data analysis, interpretation, and prediction. These techniques work with probabilistic domain-specific data modeling languages that capture key properties of a broad class of data generating processes, using Bayesian inference to synthesize probabilistic programs in these modeling languages given observed data. We provide a precise formulation of Bayesian synthesis for automatic data modeling that identifies sufficient conditions for the resulting synthesis procedure to be sound. We also derive a general class of synthesis algorithms for domain-specific languages specified by probabilistic context-free grammars and establish the soundness of our approach for these languages. We apply the techniques to automatically synthesize probabilistic programs for time series data and multivariate tabular data. We show how to analyze the structure of the synthesized programs to compute, for key qualitative properties of interest, the probability that the underlying data generating process exhibits each of these properties. Second, we translate probabilistic programs in the domain-specific language into probabilistic programs in Venture, a general-purpose probabilistic programming system. The translated Venture programs are then executed to obtain predictions of new time series data and new multivariate data records. Experimental results show that our techniques can accurately infer qualitative structure in multiple real-world data sets and outperform standard data analysis methods in forecasting and predicting new data.
Time Series Structure Discovery via Probabilistic Program Synthesis
May 22, 2017



Abstract:There is a widespread need for techniques that can discover structure from time series data. Recently introduced techniques such as Automatic Bayesian Covariance Discovery (ABCD) provide a way to find structure within a single time series by searching through a space of covariance kernels that is generated using a simple grammar. While ABCD can identify a broad class of temporal patterns, it is difficult to extend and can be brittle in practice. This paper shows how to extend ABCD by formulating it in terms of probabilistic program synthesis. The key technical ideas are to (i) represent models using abstract syntax trees for a domain-specific probabilistic language, and (ii) represent the time series model prior, likelihood, and search strategy using probabilistic programs in a sufficiently expressive language. The final probabilistic program is written in under 70 lines of probabilistic code in Venture. The paper demonstrates an application to time series clustering that involves a non-parametric extension to ABCD, experiments for interpolation and extrapolation on real-world econometric data, and improvements in accuracy over both non-parametric and standard regression baselines.
Probabilistic Programming with Gaussian Process Memoization
Jan 05, 2016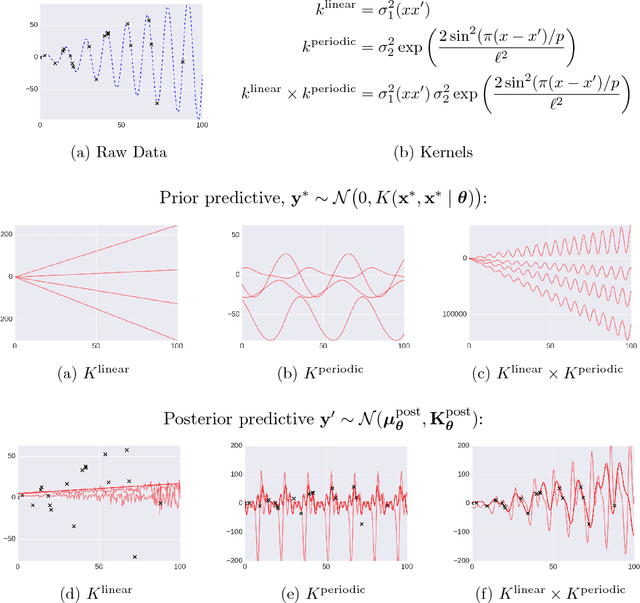
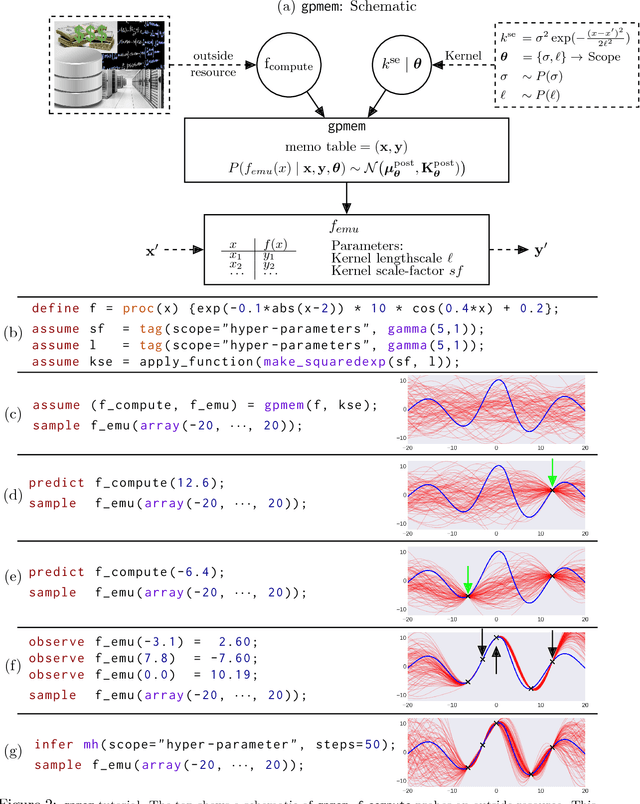
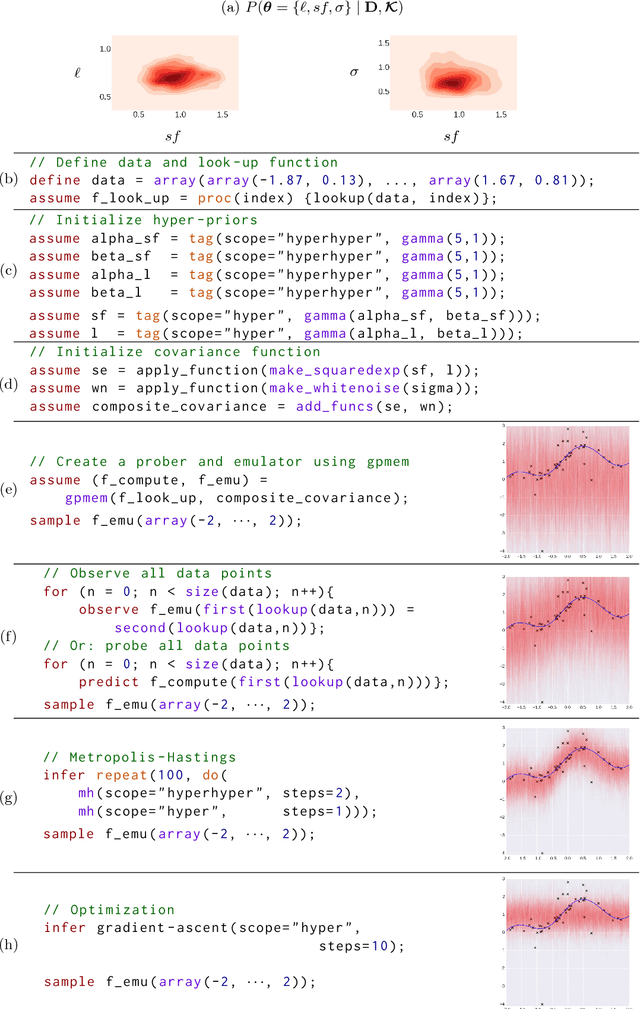
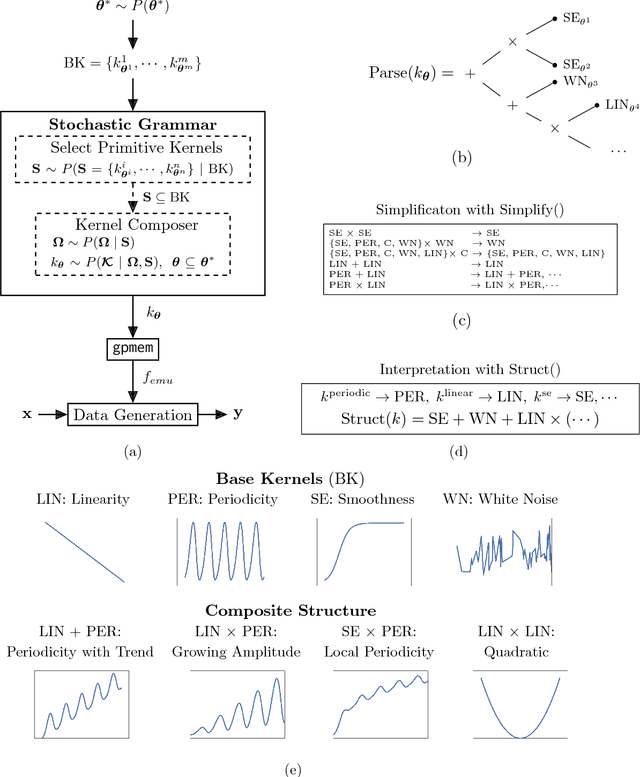
Abstract:Gaussian Processes (GPs) are widely used tools in statistics, machine learning, robotics, computer vision, and scientific computation. However, despite their popularity, they can be difficult to apply; all but the simplest classification or regression applications require specification and inference over complex covariance functions that do not admit simple analytical posteriors. This paper shows how to embed Gaussian processes in any higher-order probabilistic programming language, using an idiom based on memoization, and demonstrates its utility by implementing and extending classic and state-of-the-art GP applications. The interface to Gaussian processes, called gpmem, takes an arbitrary real-valued computational process as input and returns a statistical emulator that automatically improve as the original process is invoked and its input-output behavior is recorded. The flexibility of gpmem is illustrated via three applications: (i) robust GP regression with hierarchical hyper-parameter learning, (ii) discovering symbolic expressions from time-series data by fully Bayesian structure learning over kernels generated by a stochastic grammar, and (iii) a bandit formulation of Bayesian optimization with automatic inference and action selection. All applications share a single 50-line Python library and require fewer than 20 lines of probabilistic code each.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge