Scalable Spatiotemporal Prediction with Bayesian Neural Fields

Spatiotemporal datasets, which consist of spatially-referenced time series, are ubiquitous in many scientific and business-intelligence applications, such as air pollution monitoring, disease tracking, and cloud-demand forecasting. As modern datasets continue to increase in size and complexity, there is a growing need for new statistical methods that are flexible enough to capture complex spatiotemporal dynamics and scalable enough to handle large prediction problems. This work presents the Bayesian Neural Field (BayesNF), a domain-general statistical model for inferring rich probability distributions over a spatiotemporal domain, which can be used for data-analysis tasks including forecasting, interpolation, and variography. BayesNF integrates a novel deep neural network architecture for high-capacity function estimation with hierarchical Bayesian inference for robust uncertainty quantification. By defining the prior through a sequence of smooth differentiable transforms, posterior inference is conducted on large-scale data using variationally learned surrogates trained via stochastic gradient descent. We evaluate BayesNF against prominent statistical and machine-learning baselines, showing considerable improvements on diverse prediction problems from climate and public health datasets that contain tens to hundreds of thousands of measurements. The paper is accompanied with an open-source software package (https://github.com/google/bayesnf) that is easy-to-use and compatible with modern GPU and TPU accelerators on the JAX machine learning platform.

Time Series Structure Discovery via Probabilistic Program Synthesis

There is a widespread need for techniques that can discover structure from time series data. Recently introduced techniques such as Automatic Bayesian Covariance Discovery (ABCD) provide a way to find structure within a single time series by searching through a space of covariance kernels that is generated using a simple grammar. While ABCD can identify a broad class of temporal patterns, it is difficult to extend and can be brittle in practice. This paper shows how to extend ABCD by formulating it in terms of probabilistic program synthesis. The key technical ideas are to (i) represent models using abstract syntax trees for a domain-specific probabilistic language, and (ii) represent the time series model prior, likelihood, and search strategy using probabilistic programs in a sufficiently expressive language. The final probabilistic program is written in under 70 lines of probabilistic code in Venture. The paper demonstrates an application to time series clustering that involves a non-parametric extension to ABCD, experiments for interpolation and extrapolation on real-world econometric data, and improvements in accuracy over both non-parametric and standard regression baselines.

Probabilistic Search for Structured Data via Probabilistic Programming and Nonparametric Bayes

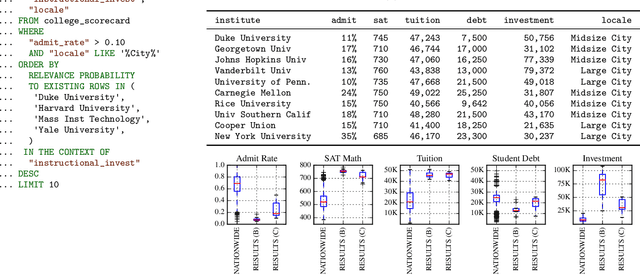
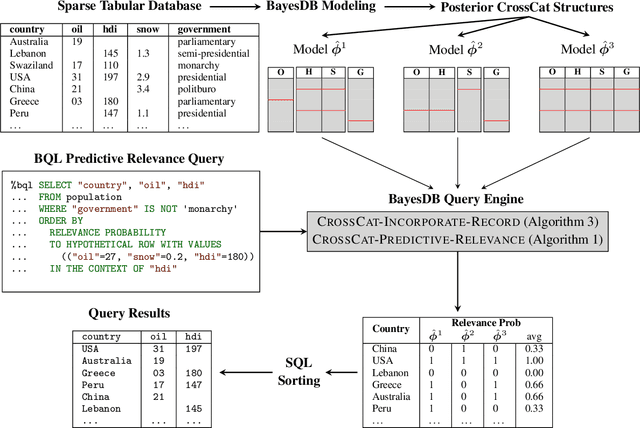
Databases are widespread, yet extracting relevant data can be difficult. Without substantial domain knowledge, multivariate search queries often return sparse or uninformative results. This paper introduces an approach for searching structured data based on probabilistic programming and nonparametric Bayes. Users specify queries in a probabilistic language that combines standard SQL database search operators with an information theoretic ranking function called predictive relevance. Predictive relevance can be calculated by a fast sparse matrix algorithm based on posterior samples from CrossCat, a nonparametric Bayesian model for high-dimensional, heterogeneously-typed data tables. The result is a flexible search technique that applies to a broad class of information retrieval problems, which we integrate into BayesDB, a probabilistic programming platform for probabilistic data analysis. This paper demonstrates applications to databases of US colleges, global macroeconomic indicators of public health, and classic cars. We found that human evaluators often prefer the results from probabilistic search to results from a standard baseline.

Detecting Dependencies in Sparse, Multivariate Databases Using Probabilistic Programming and Non-parametric Bayes

Datasets with hundreds of variables and many missing values are commonplace. In this setting, it is both statistically and computationally challenging to detect true predictive relationships between variables and also to suppress false positives. This paper proposes an approach that combines probabilistic programming, information theory, and non-parametric Bayes. It shows how to use Bayesian non-parametric modeling to (i) build an ensemble of joint probability models for all the variables; (ii) efficiently detect marginal independencies; and (iii) estimate the conditional mutual information between arbitrary subsets of variables, subject to a broad class of constraints. Users can access these capabilities using BayesDB, a probabilistic programming platform for probabilistic data analysis, by writing queries in a simple, SQL-like language. This paper demonstrates empirically that the method can (i) detect context-specific (in)dependencies on challenging synthetic problems and (ii) yield improved sensitivity and specificity over baselines from statistics and machine learning, on a real-world database of over 300 sparsely observed indicators of macroeconomic development and public health.

Probabilistic Data Analysis with Probabilistic Programming

Probabilistic techniques are central to data analysis, but different approaches can be difficult to apply, combine, and compare. This paper introduces composable generative population models (CGPMs), a computational abstraction that extends directed graphical models and can be used to describe and compose a broad class of probabilistic data analysis techniques. Examples include hierarchical Bayesian models, multivariate kernel methods, discriminative machine learning, clustering algorithms, dimensionality reduction, and arbitrary probabilistic programs. We also demonstrate the integration of CGPMs into BayesDB, a probabilistic programming platform that can express data analysis tasks using a modeling language and a structured query language. The practical value is illustrated in two ways. First, CGPMs are used in an analysis that identifies satellite data records which probably violate Kepler's Third Law, by composing causal probabilistic programs with non-parametric Bayes in under 50 lines of probabilistic code. Second, for several representative data analysis tasks, we report on lines of code and accuracy measurements of various CGPMs, plus comparisons with standard baseline solutions from Python and MATLAB libraries.