Robust Autonomy Emerges from Self-Play

Self-play has powered breakthroughs in two-player and multi-player games. Here we show that self-play is a surprisingly effective strategy in another domain. We show that robust and naturalistic driving emerges entirely from self-play in simulation at unprecedented scale -- 1.6~billion~km of driving. This is enabled by Gigaflow, a batched simulator that can synthesize and train on 42 years of subjective driving experience per hour on a single 8-GPU node. The resulting policy achieves state-of-the-art performance on three independent autonomous driving benchmarks. The policy outperforms the prior state of the art when tested on recorded real-world scenarios, amidst human drivers, without ever seeing human data during training. The policy is realistic when assessed against human references and achieves unprecedented robustness, averaging 17.5 years of continuous driving between incidents in simulation.

Reinforcement Learning for Long-Horizon Interactive LLM Agents

Interactive digital agents (IDAs) leverage APIs of stateful digital environments to perform tasks in response to user requests. While IDAs powered by instruction-tuned large language models (LLMs) can react to feedback from interface invocations in multi-step exchanges, they have not been trained in their respective digital environments. Prior methods accomplish less than half of tasks in sophisticated benchmarks such as AppWorld. We present a reinforcement learning (RL) approach that trains IDAs directly in their target environments. We formalize this training as a partially observable Markov decision process and derive LOOP, a data- and memory-efficient variant of proximal policy optimization. LOOP uses no value network and maintains exactly one copy of the underlying LLM in memory, making its implementation straightforward and as memory-efficient as fine-tuning a single LLM. A 32-billion-parameter agent trained with LOOP in the AppWorld environment outperforms the much larger OpenAI o1 agent by 9 percentage points (15% relative). To our knowledge, this is the first reported application of RL to IDAs that interact with a stateful, multi-domain, multi-app environment via direct API calls. Our analysis sheds light on the effectiveness of RL in this area, showing that the agent learns to consult the API documentation, avoid unwarranted assumptions, minimize confabulation, and recover from setbacks.

Estimators of Entropy and Information via Inference in Probabilistic Models

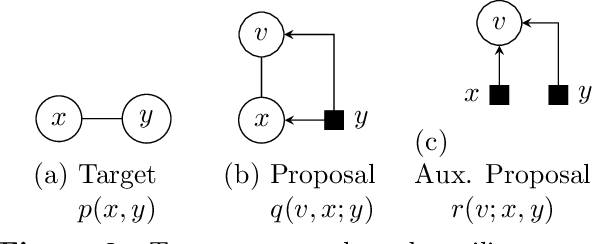
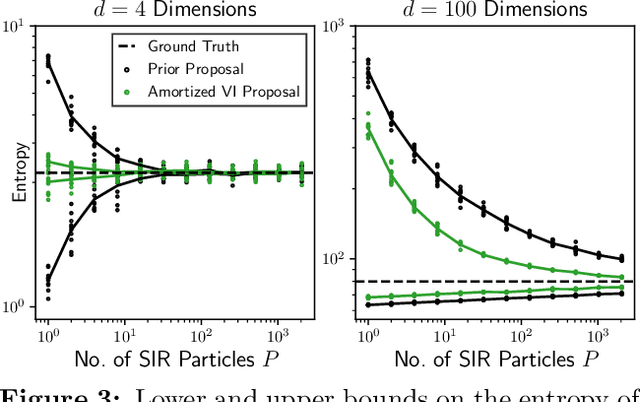
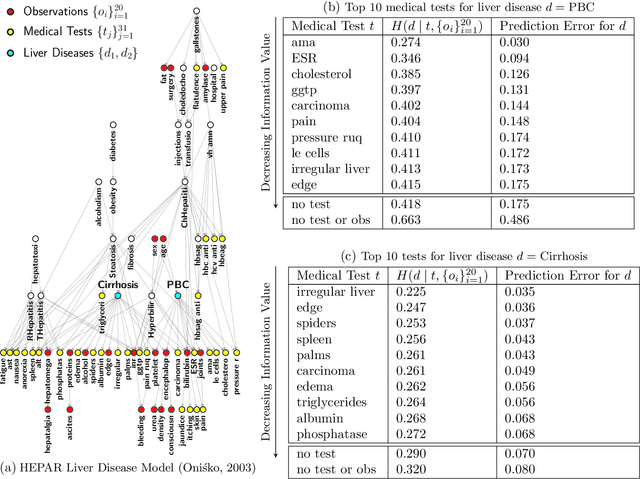
Estimating information-theoretic quantities such as entropy and mutual information is central to many problems in statistics and machine learning, but challenging in high dimensions. This paper presents estimators of entropy via inference (EEVI), which deliver upper and lower bounds on many information quantities for arbitrary variables in a probabilistic generative model. These estimators use importance sampling with proposal distribution families that include amortized variational inference and sequential Monte Carlo, which can be tailored to the target model and used to squeeze true information values with high accuracy. We present several theoretical properties of EEVI and demonstrate scalability and efficacy on two problems from the medical domain: (i) in an expert system for diagnosing liver disorders, we rank medical tests according to how informative they are about latent diseases, given a pattern of observed symptoms and patient attributes; and (ii) in a differential equation model of carbohydrate metabolism, we find optimal times to take blood glucose measurements that maximize information about a diabetic patient's insulin sensitivity, given their meal and medication schedule.

Recursive Monte Carlo and Variational Inference with Auxiliary Variables

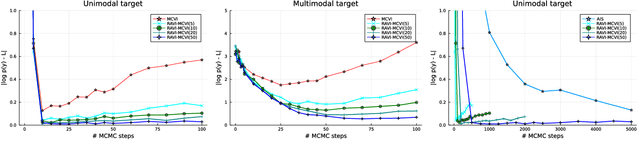
A key challenge in applying Monte Carlo and variational inference (VI) is the design of proposals and variational families that are flexible enough to closely approximate the posterior, but simple enough to admit tractable densities and variational bounds. This paper presents recursive auxiliary-variable inference (RAVI), a new framework for exploiting flexible proposals, for example based on involved simulations or stochastic optimization, within Monte Carlo and VI algorithms. The key idea is to estimate intractable proposal densities via meta-inference: additional Monte Carlo or variational inference targeting the proposal, rather than the model. RAVI generalizes and unifies several existing methods for inference with expressive approximating families, which we show correspond to specific choices of meta-inference algorithm, and provides new theory for analyzing their bias and variance. We illustrate RAVI's design framework and theorems by using them to analyze and improve upon Salimans et al. (2015)'s Markov Chain Variational Inference, and to design a novel sampler for Dirichlet process mixtures, achieving state-of-the-art results on a standard benchmark dataset from astronomy and on a challenging data-cleaning task with Medicare hospital data.

3DP3: 3D Scene Perception via Probabilistic Programming

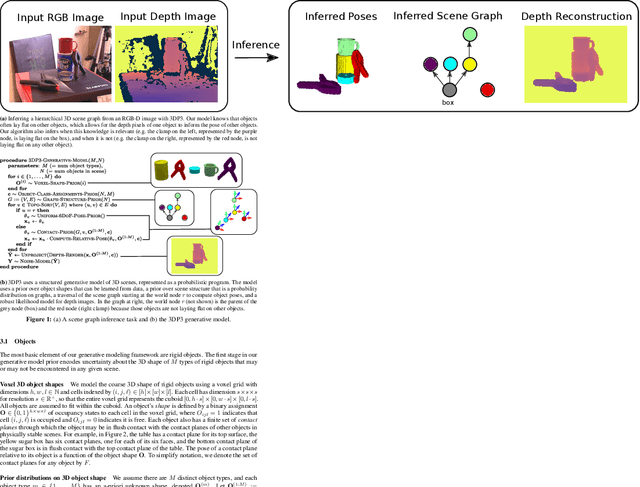
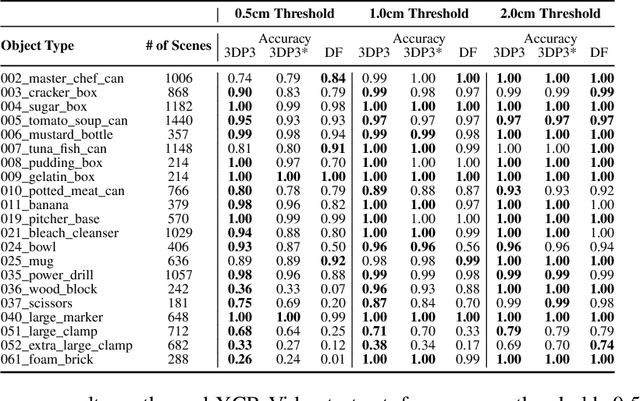
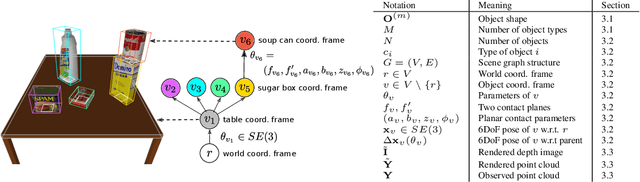
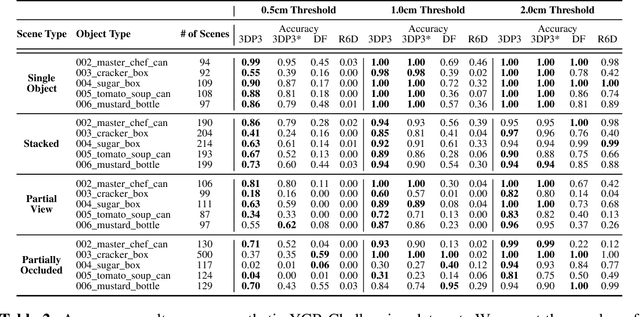
We present 3DP3, a framework for inverse graphics that uses inference in a structured generative model of objects, scenes, and images. 3DP3 uses (i) voxel models to represent the 3D shape of objects, (ii) hierarchical scene graphs to decompose scenes into objects and the contacts between them, and (iii) depth image likelihoods based on real-time graphics. Given an observed RGB-D image, 3DP3's inference algorithm infers the underlying latent 3D scene, including the object poses and a parsimonious joint parametrization of these poses, using fast bottom-up pose proposals, novel involutive MCMC updates of the scene graph structure, and, optionally, neural object detectors and pose estimators. We show that 3DP3 enables scene understanding that is aware of 3D shape, occlusion, and contact structure. Our results demonstrate that 3DP3 is more accurate at 6DoF object pose estimation from real images than deep learning baselines and shows better generalization to challenging scenes with novel viewpoints, contact, and partial observability.