Recursive Monte Carlo and Variational Inference with Auxiliary Variables

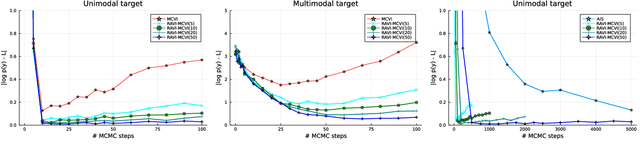
A key challenge in applying Monte Carlo and variational inference (VI) is the design of proposals and variational families that are flexible enough to closely approximate the posterior, but simple enough to admit tractable densities and variational bounds. This paper presents recursive auxiliary-variable inference (RAVI), a new framework for exploiting flexible proposals, for example based on involved simulations or stochastic optimization, within Monte Carlo and VI algorithms. The key idea is to estimate intractable proposal densities via meta-inference: additional Monte Carlo or variational inference targeting the proposal, rather than the model. RAVI generalizes and unifies several existing methods for inference with expressive approximating families, which we show correspond to specific choices of meta-inference algorithm, and provides new theory for analyzing their bias and variance. We illustrate RAVI's design framework and theorems by using them to analyze and improve upon Salimans et al. (2015)'s Markov Chain Variational Inference, and to design a novel sampler for Dirichlet process mixtures, achieving state-of-the-art results on a standard benchmark dataset from astronomy and on a challenging data-cleaning task with Medicare hospital data.