Hierarchical Infinite Relational Model
Paper and Code
Aug 16, 2021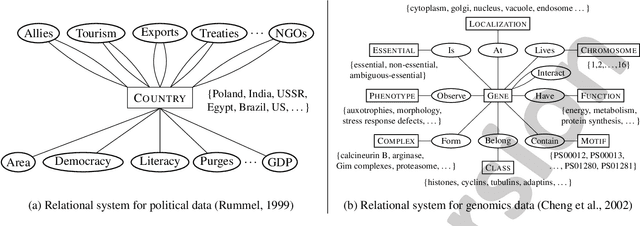
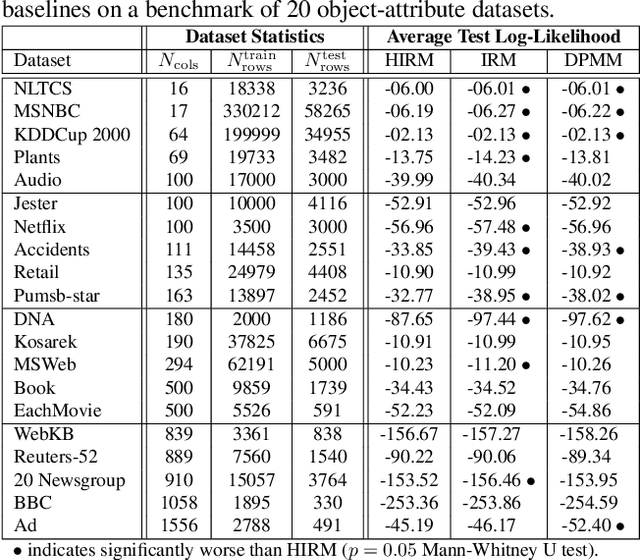

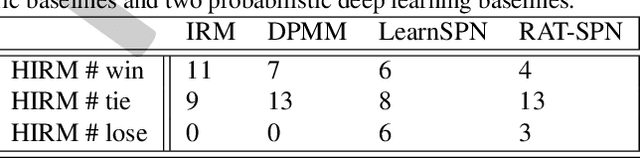
This paper describes the hierarchical infinite relational model (HIRM), a new probabilistic generative model for noisy, sparse, and heterogeneous relational data. Given a set of relations defined over a collection of domains, the model first infers multiple non-overlapping clusters of relations using a top-level Chinese restaurant process. Within each cluster of relations, a Dirichlet process mixture is then used to partition the domain entities and model the probability distribution of relation values. The HIRM generalizes the standard infinite relational model and can be used for a variety of data analysis tasks including dependence detection, clustering, and density estimation. We present new algorithms for fully Bayesian posterior inference via Gibbs sampling. We illustrate the efficacy of the method on a density estimation benchmark of twenty object-attribute datasets with up to 18 million cells and use it to discover relational structure in real-world datasets from politics and genomics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge