Program Analysis of Probabilistic Programs

Probabilistic programming is a growing area that strives to make statistical analysis more accessible, by separating probabilistic modelling from probabilistic inference. In practice this decoupling is difficult. No single inference algorithm can be used as a probabilistic programming back-end that is simultaneously reliable, efficient, black-box, and general. Probabilistic programming languages often choose a single algorithm to apply to a given problem, thus inheriting its limitations. While substantial work has been done both to formalise probabilistic programming and to improve efficiency of inference, there has been little work that makes use of the available program structure, by formally analysing it, to better utilise the underlying inference algorithm. This dissertation presents three novel techniques (both static and dynamic), which aim to improve probabilistic programming using program analysis. The techniques analyse a probabilistic program and adapt it to make inference more efficient, sometimes in a way that would have been tedious or impossible to do by hand.

On the Unreasonable Effectiveness of Feature propagation in Learning on Graphs with Missing Node Features

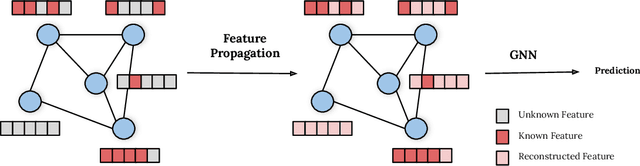
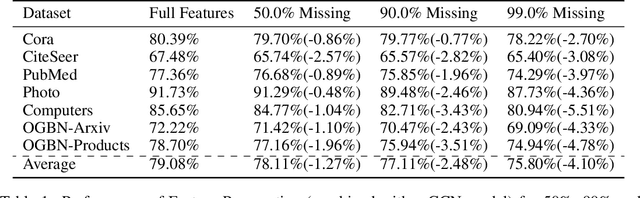
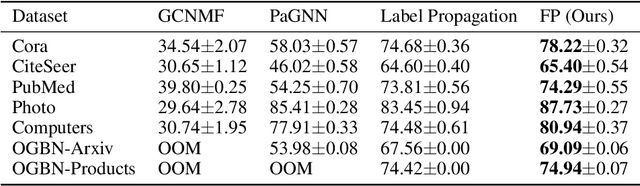
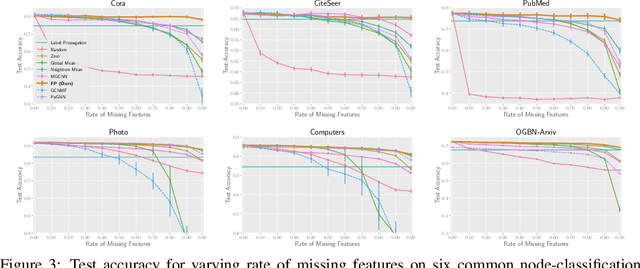
While Graph Neural Networks (GNNs) have recently become the de facto standard for modeling relational data, they impose a strong assumption on the availability of the node or edge features of the graph. In many real-world applications, however, features are only partially available; for example, in social networks, age and gender are available only for a small subset of users. We present a general approach for handling missing features in graph machine learning applications that is based on minimization of the Dirichlet energy and leads to a diffusion-type differential equation on the graph. The discretization of this equation produces a simple, fast and scalable algorithm which we call Feature Propagation. We experimentally show that the proposed approach outperforms previous methods on seven common node-classification benchmarks and can withstand surprisingly high rates of missing features: on average we observe only around 4% relative accuracy drop when 99% of the features are missing. Moreover, it takes only 10 seconds to run on a graph with $\sim$2.5M nodes and $\sim$123M edges on a single GPU.

Conditional independence by typing

A central goal of probabilistic programming languages (PPLs) is to separate modelling from inference. However, this goal is hard to achieve in practice. Users are often forced to re-write their models in order to improve efficiency of inference or meet restrictions imposed by the PPL. Conditional independence (CI) relationships among parameters are a crucial aspect of probabilistic models that captures a qualitative summary of the specified model and can facilitate more efficient inference. We present an information flow type system for probabilistic programming that captures conditional independence (CI) relationships, and show that, for a well-typed program in our system, the distribution it implements is guaranteed to have certain CI-relationships. Further, by using type inference, we can statically \emph{deduce} which CI-properties are present in a specified model. As a practical application, we consider the problem of how to perform inference on models with mixed discrete and continuous parameters. Inference on such models is challenging in many existing PPLs, but can be improved through a workaround, where the discrete parameters are used \textit{implicitly}, at the expense of manual model re-writing. We present a source-to-source semantics-preserving transformation, which uses our CI-type system to automate this workaround by eliminating the discrete parameters from a probabilistic program. The resulting program can be seen as a hybrid inference algorithm on the original program, where continuous parameters can be drawn using efficient gradient-based inference methods, while the discrete parameters are drawn using variable elimination. We implement our CI-type system and its example application in SlicStan: a compositional variant of Stan.

Automatic Reparameterisation of Probabilistic Programs

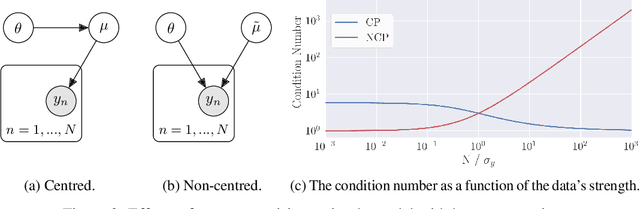
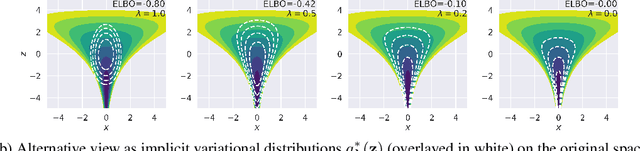
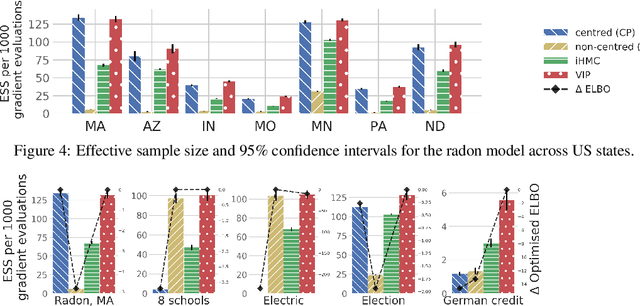
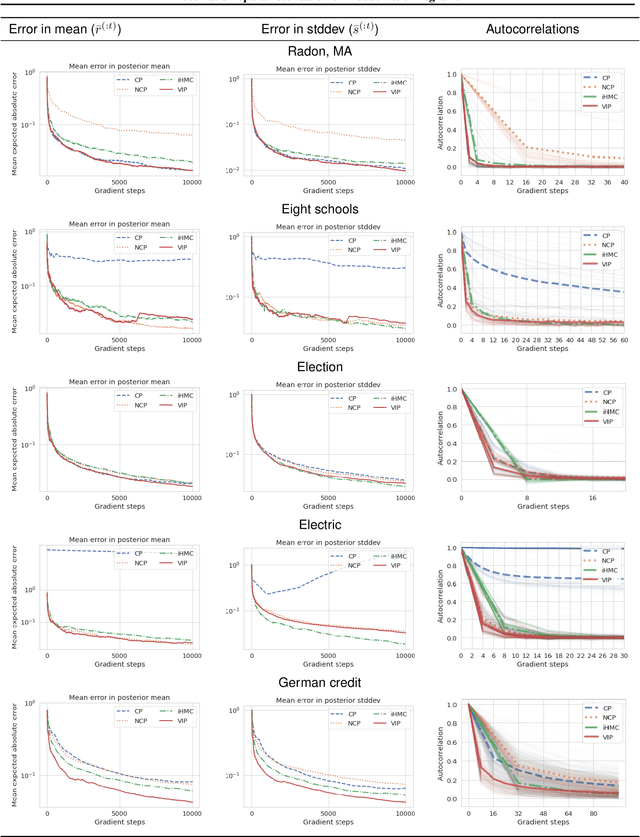
Probabilistic programming has emerged as a powerful paradigm in statistics, applied science, and machine learning: by decoupling modelling from inference, it promises to allow modellers to directly reason about the processes generating data. However, the performance of inference algorithms can be dramatically affected by the parameterisation used to express a model, requiring users to transform their programs in non-intuitive ways. We argue for automating these transformations, and demonstrate that mechanisms available in recent modeling frameworks can implement non-centring and related reparameterisations. This enables new inference algorithms, and we propose two: a simple approach using interleaved sampling and a novel variational formulation that searches over a continuous space of parameterisations. We show that these approaches enable robust inference across a range of models, and can yield more efficient samplers than the best fixed parameterisation.

Effect Handling for Composable Program Transformations in Edward2

Algebraic effects and handlers have emerged in the programming languages community as a convenient, modular abstraction for controlling computational effects. They have found several applications including concurrent programming, meta programming, and more recently, probabilistic programming, as part of Pyro's Poutines library. We investigate the use of effect handlers as a lightweight abstraction for implementing probabilistic programming languages (PPLs). We interpret the existing design of Edward2 as an accidental implementation of an effect-handling mechanism, and extend that design to support nested, composable transformations. We demonstrate that this enables straightforward implementation of sophisticated model transformations and inference algorithms.

Probabilistic Programming with Densities in SlicStan: Efficient, Flexible and Deterministic

Stan is a probabilistic programming language that has been increasingly used for real-world scalable projects. However, to make practical inference possible, the language sacrifices some of its usability by adopting a block syntax, which lacks compositionality and flexible user-defined functions. Moreover, the semantics of the language has been mainly given in terms of intuition about implementation, and has not been formalised. This paper provides a formal treatment of the Stan language, and introduces the probabilistic programming language SlicStan --- a compositional, self-optimising version of Stan. Our main contributions are: (1) the formalisation of a core subset of Stan through an operational density-based semantics; (2) the design and semantics of the Stan-like language SlicStan, which facilities better code reuse and abstraction through its compositional syntax, more flexible functions, and information-flow type system; and (3) a formal, semantic-preserving procedure for translating SlicStan to Stan.