Dependent Multinomial Models Made Easy: Stick Breaking with the Pólya-Gamma Augmentation
Paper and Code
Jun 18, 2015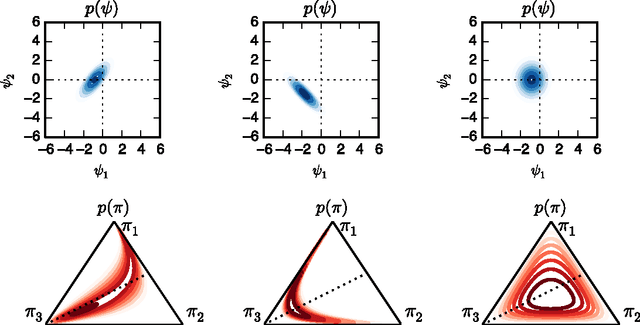
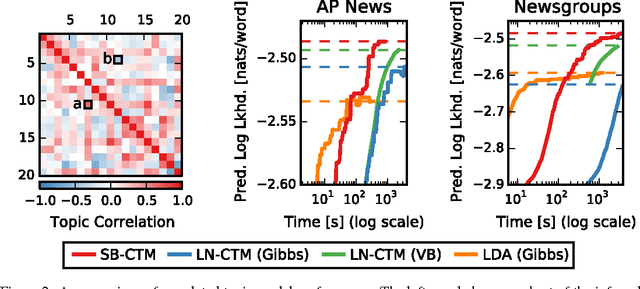
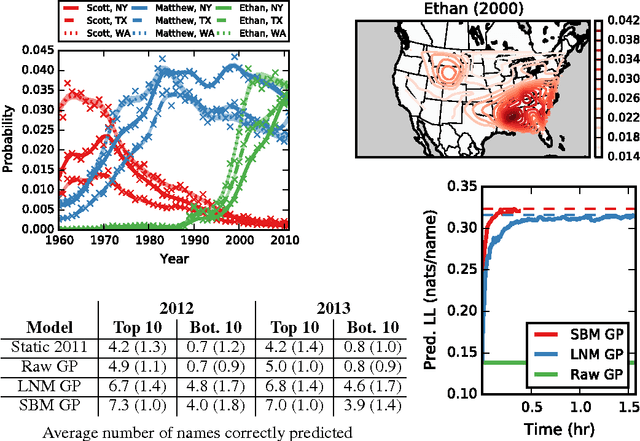
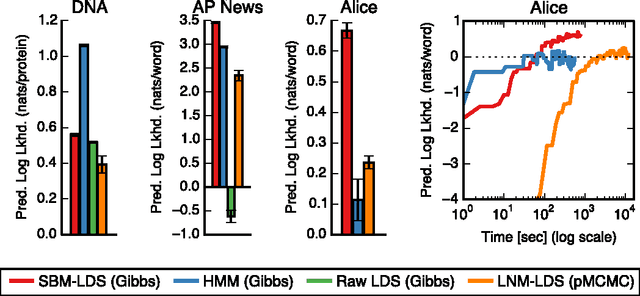
Many practical modeling problems involve discrete data that are best represented as draws from multinomial or categorical distributions. For example, nucleotides in a DNA sequence, children's names in a given state and year, and text documents are all commonly modeled with multinomial distributions. In all of these cases, we expect some form of dependency between the draws: the nucleotide at one position in the DNA strand may depend on the preceding nucleotides, children's names are highly correlated from year to year, and topics in text may be correlated and dynamic. These dependencies are not naturally captured by the typical Dirichlet-multinomial formulation. Here, we leverage a logistic stick-breaking representation and recent innovations in P\'olya-gamma augmentation to reformulate the multinomial distribution in terms of latent variables with jointly Gaussian likelihoods, enabling us to take advantage of a host of Bayesian inference techniques for Gaussian models with minimal overhead.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge